Дифференциальное уравнение первого порядка имеет вид F(x, y, y’) или y’ = f(x, y) (разрешенное относительно y).
Решением дифференциального уравнения называется функция у(x), которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения можно записать в явном виде 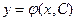 или в виде общего интеграла Ф(x, y, C) = 0, где С – произвольная постоянная.
или в виде общего интеграла Ф(x, y, C) = 0, где С – произвольная постоянная.
Теорема. Если функция f(x, y) непрерывна в некоторой области, содержащей точку (x0, y0) и имеет там ограниченную частную производную по y, то существует единственное решение уравнения 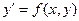 , удовлетворяющее условию Коши: y = y0 при x = x0.
, удовлетворяющее условию Коши: y = y0 при x = x0.
Уравнения, допускающие аналитическое решение:
1) Дифференциальные уравнения с разделяющимися переменными
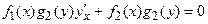
путем деления на 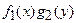 допускают интегрирование
допускают интегрирование
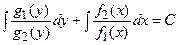 .
.
2) Однородное дифференциальное уравнение 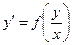 с помощью подстановки y=xz приводится к уравнению с разделяющимися переменными
с помощью подстановки y=xz приводится к уравнению с разделяющимися переменными 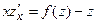 .
.
3) Линейное дифференциальное уравнение 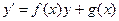 . Решение ищем в виде
. Решение ищем в виде 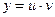 , где v удовлетворяет однородному линейному дифференциальному уравнению
, где v удовлетворяет однородному линейному дифференциальному уравнению
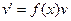
Для u получим уравнение 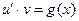 .
.
Интегрируя последовательно уравнения для u и v получим решение

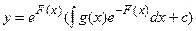 , где
, где 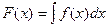
4) Уравнение Бернулли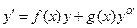 . Замена
. Замена 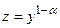 приводит к линейному дифференциальному уравнению
приводит к линейному дифференциальному уравнению 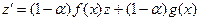
5) Дифференциальные уравнения в полных дифференциалах
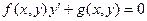 , где
, где 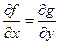
Общий интеграл: 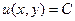 , где функция u определяется из системы
, где функция u определяется из системы 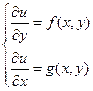
Интегрируя первое уравнение, имеем 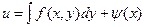 . Подстановка этого выражения во второе уравнение позволяет найти функцию
. Подстановка этого выражения во второе уравнение позволяет найти функцию 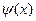 , а затем u.
, а затем u.
Пример 1. Решить уравнение
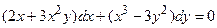
Решение. Так как 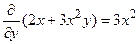 ,
, 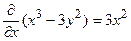 , то данное уравнение является уравнением в полных дифференциалах. Найдем такую функцию u(x, y), что
, то данное уравнение является уравнением в полных дифференциалах. Найдем такую функцию u(x, y), что 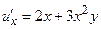 ;
; 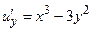
Первое из этих уравнений проинтегрируем по х, считая y постоянным; при этом вместо постоянной интегрирования поставим 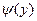 - неизвестную функцию от y:
- неизвестную функцию от y:
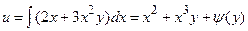
Подставляя это выражение во второе уравнение, найдем:
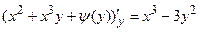 ,
,
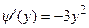 ;
; 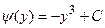 .
.
Следовательно, можно взять 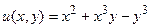 и общее решение исходного уравнения будет иметь вид:
и общее решение исходного уравнения будет иметь вид:
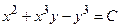
Дифференциальные уравнения высших порядков.
Общее решение дифференциального уравнения n – го порядка
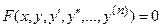 ,
,
имеет вид 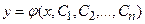 , где
, где 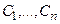 - произвольные постоянные.
- произвольные постоянные.
Простейшие дифференциальные уравнения, допускающие понижение порядка:
1) Уравнение 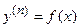 решается последовательным n – кратным интегрированием правой части,
решается последовательным n – кратным интегрированием правой части,
2) Уравнение 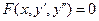 , не содержащее явно y, с помощью подстановки
, не содержащее явно y, с помощью подстановки 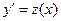 приводится к дифференциальному уравнению 1-го порядка
приводится к дифференциальному уравнению 1-го порядка 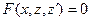 ,
,
3) Уравнение 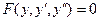 , не содержащее явно x. Подстановка
, не содержащее явно x. Подстановка 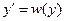 (y играет роль независимой переменной) с учетом равенств
(y играет роль независимой переменной) с учетом равенств 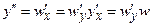 приводит уравнение к уравнению 1-го порядка
приводит уравнение к уравнению 1-го порядка
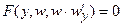 .
.
Линейное однородное дифференциальное уравнение n-го порядка (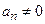 )
)
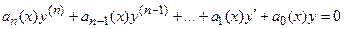
Общее решение линейного однородного дифференциального уравнения:
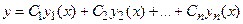 ,
,
где 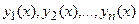 - линейно-независимые частные решения (фундаментальная система решений) этого уравнения;
- линейно-независимые частные решения (фундаментальная система решений) этого уравнения; 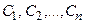 - произвольные постоянные.
- произвольные постоянные.
Линейное неоднородное дифференциальное уравнение n-го порядка (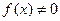 )
)
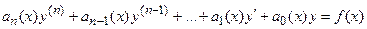 .
.
Общее решение
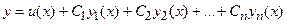 ,
,
где u(x) - частное решение неоднородного уравнения, а 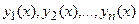 - фундаментальная система решений соответствующего однородного уравнения.
- фундаментальная система решений соответствующего однородного уравнения.
Если 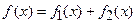 , то частное решение
, то частное решение 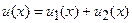 , где
, где 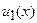 и
и 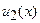 - частные решения, соответствующие отдельным слагаемым
- частные решения, соответствующие отдельным слагаемым 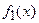 и
и 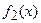 в правой части дифференциального уравнения.
в правой части дифференциального уравнения.
1. Линейные уравнения n-го порядка с постоянными коэффициентами.
Линейное однородное уравнение n-го порядка с постоянными коэффициентами (a0, a1, a2, an – числа) имеет вид:
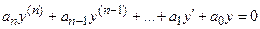

Корни характеристического уравнения:
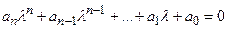
определяют следующие слагаемые в общем решении:
а) действительный простой корень 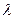 дает слагаемое
дает слагаемое 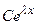 ;
;
б) действительный корень 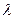 кратности m дает слагаемое
кратности m дает слагаемое
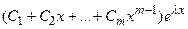 .
.
в) пара комплексно-сопряженных корней 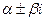 дает слагаемое
дает слагаемое
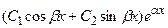
г) пара комплексно-сопряженных корней 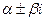 кратности m дает слагаемое
кратности m дает слагаемое 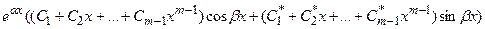 .
.
Например, если все корни 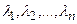 характеристического уравнения действительны и различны, то дифференциальное уравнение имеет общее решение
характеристического уравнения действительны и различны, то дифференциальное уравнение имеет общее решение
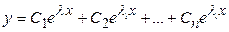
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.
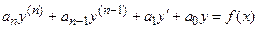
Если 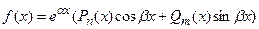 , где
, где 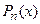 и
и 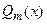 - многочлены n-ой и m-ой степени, то частное решение ищут методом неопределенных коэффициентов в виде
- многочлены n-ой и m-ой степени, то частное решение ищут методом неопределенных коэффициентов в виде
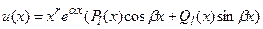 ;
;
Здесь r – кратность корня 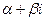 в характеристическом уравнении (если такого корня нет, то r = 0);
в характеристическом уравнении (если такого корня нет, то r = 0);
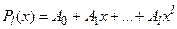 и
и 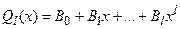 - степени
- степени 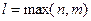 . Неопределенные коэффициенты
. Неопределенные коэффициенты 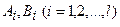 находятся из системы линейных алгебраических уравнений, путем приравнивания коэффициентов при одинаковых степенях x в обеих частях исходного уравнения после подстановки в него u(x) вместо y. Если в выражение для f(x) входит хотя бы одна из функций
находятся из системы линейных алгебраических уравнений, путем приравнивания коэффициентов при одинаковых степенях x в обеих частях исходного уравнения после подстановки в него u(x) вместо y. Если в выражение для f(x) входит хотя бы одна из функций 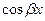 или
или 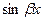 , то в u(x) надо всегда вводить обе функции.
, то в u(x) надо всегда вводить обе функции.
Пример 2. Решить уравнение
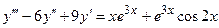
Решение. Составляем характеристическое уравнение 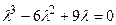 ;
; 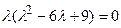 .
.
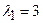 - двукратный корень,
- двукратный корень, 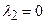 - кратности 1.
- кратности 1.
Поэтому общее решение однородного уравнения имеет вид:
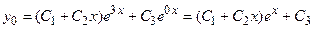
Правая часть исходного уравнения состоит из двух слагаемых. Для первого уравнения
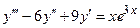 (*)
(*)
частное решение будет иметь вид 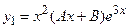 , так как имеем кратный корень. Подставив y1 в уравнение (*), найдем
, так как имеем кратный корень. Подставив y1 в уравнение (*), найдем 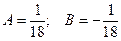 .
.
Для второго уравнения 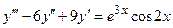 (**) частное решение будем искать в виде
(**) частное решение будем искать в виде
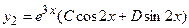 .
.
Подставив y2 в уравнение (**), найдем 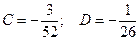
Тогда общее решение исходного уравнения y = y0 + y1 + y2, где y0, y1, y2 уже найдены.
Упражнения.
Найти и построить интегральную кривую, проходящую через точку М:
a) 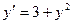 , М (1;0);
, М (1;0);
b) 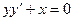 , М (-2;-3);
, М (-2;-3);
c) 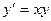 , М (0;1);
, М (0;1);
d) 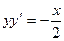 , М (4;2);
, М (4;2);
e) 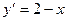 , М (2;-1);
, М (2;-1);
f) 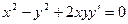 , М (2;1);
, М (2;1);
g) 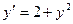 , М (1;2);
, М (1;2);
h) 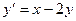 , М (0;1).
, М (0;1).
Найти общее решение дифференциального уравнения:
a) 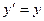 ; b
; b 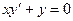 ;
;
c) 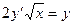 ; d)
; d) 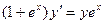 ;
;
e) 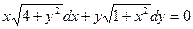 ;
;
f) 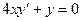 ; g)
; g) 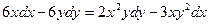 ;
;
h) 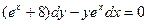 .
.
Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию:
a) 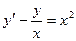 ,
, 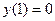 ;
;
b) 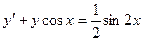 ,
, 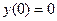 ;
;
c) 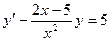 ,
, 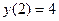 ;
;
d) 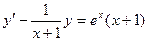 ,
, 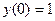 ;
;
e) 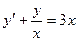 ,
, 
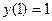 ;
;
f) 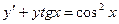 ,
, 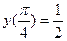 ;
;
g) 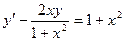 ,
, 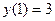 ;
;
h) 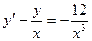 ,
, 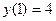 .
.
Найти общий интеграл однородного уравнения:
a) 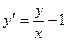 ; b)
; b) 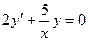 ;
;
c) 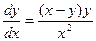 ; d)
; d) 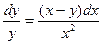 ;
;
e) 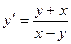 ; f)
; f) 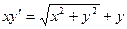 ;
;
g) 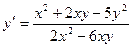 ; h)
; h) 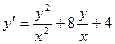 .
.
Решить линейные однородные уравнения второго порядка:
a) 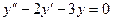 ; b)
; b) 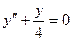 ;
;
c) 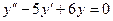 ; d)
; d) 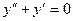 ;
;
e) 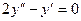 ; f)
; f) 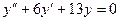 ;
;
g) 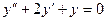 ; h)
; h) 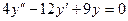 .
.
Решить линейные неоднородные уравнения:
a) 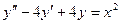 ; b)
; b) 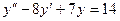 ;
;
c) 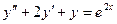 ; d)
; d) 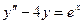 .
.
Ряды.
Числовые ряды
Выражение 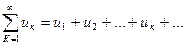 называется числовым рядом;
называется числовым рядом;
uк – общим числом ряда;
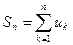 - n -ной частичной суммой ряда.
- n -ной частичной суммой ряда.
Ряд называется сходящимся, а S – суммой ряда, если 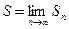 . Если
. Если 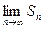 не существует или не ограничен, то ряд называется расходящимся.
не существует или не ограничен, то ряд называется расходящимся.
Свойства сходящихся рядов:
1. Необходимый признак сходимости ряда: если ряд 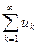 сходится, то
сходится, то 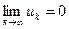 (если
(если 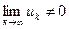 , то ряд расходится).
, то ряд расходится).
2. Члены сходящегося ряда можно группировать в порядке следования, полученный новый ряд сходится и имеет ту же сумму.
3. Если сходятся ряды 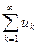 и
и 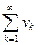 , то сходится ряд
, то сходится ряд
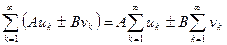 .
.
Признаки сходимости рядов с положительными членами:
1. Признак сравнения.
Если 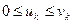 для всех
для всех 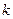 > N, то из сходимости ряда
> N, то из сходимости ряда 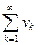 следует сходимость ряда
следует сходимость ряда 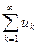 , а из расходимости ряда
, а из расходимости ряда 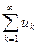 - расходимость ряда
- расходимость ряда 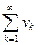 .
.
Для эффективного применения признака сравнения необходимо иметь «запас» рядов, сходимость или расходимость которых твердо установлена. Некоторые из таких рядов приведены в таблице:
| Сходящиеся ряды | Расходящиеся ряды |
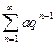 геометрический ряд со знаменателем 0<q<1 геометрический ряд со знаменателем 0<q<1 | 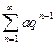 геометрический ряд со знаменателем q геометрический ряд со знаменателем q  1 1 |
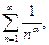 α >1 α >1 | 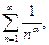 (0 < (0 < 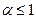 , α=1 – гармонический ряд) , α=1 – гармонический ряд) |
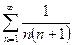 | 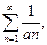 при а>0 при а>0 |
2. Признак сравнения в предельной форме.
Если для знакоположительных рядов 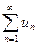 и
и 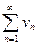 существует конечный предел
существует конечный предел 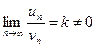 , то из сходимости второго ряда вытекает сходимость первого ряда. Если
, то из сходимости второго ряда вытекает сходимость первого ряда. Если 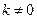 (но возможно
(но возможно 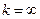 ), то из расходимости второго ряда следует расходимость первого.
), то из расходимости второго ряда следует расходимость первого.
Если 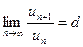 , то при
, то при 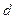 сходится, а при
сходится, а при 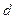 > 1 – расходится.
> 1 – расходится.
Если 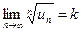 , где k – число, то при k < 1 ряд
, где k – число, то при k < 1 ряд 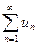 сходится, а при k > 1 – расходится.
сходится, а при k > 1 – расходится.
5. Интегральный признак Маклорена – Коши:
Ряд с общим членом un = f(n) сходится, если f(x) – монотонноубывающая функция, определена для всех 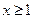 и сходится несобственный интеграл
и сходится несобственный интеграл 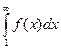 .
.
Если несобственный интеграл расходится, то и ряд расходится.
Пример 1. Исследовать сходимость ряда: 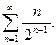
Решение. Проверим выполнение необходимого признака сходимости, для чего найдем предел его общего члена:
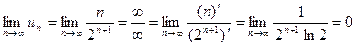 .
.
Следовательно, необходимое условие сходимости выполнено. Дальнейшее исследование ряда на сходимость проведем с помощью признака Даламбера.
Вычисли 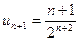 , найдем:
, найдем:
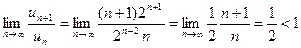 , следовательно, по признаку Даламбера ряд сходится.
, следовательно, по признаку Даламбера ряд сходится.
 2015-10-22
2015-10-22 11975
11975
