Элементы теории корреляций

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует определенной значение другой. Однако, в практической деятельности часто встречаются переменные величины, которые являются зависимыми, причем каждому значению одной из них соответствует не одно, а некоторое множество значений другой.

Переменные X и Y связаны статистически, если каждому значению одной из них соответствует распределение другой, меняющейся с изменением первой и по вариантам, и по частотам. Как правило, статистически зависимые величины задаются с помощью корреляционной таблицы:

y x	y 1	y 2	…	yj	…	yt	Всего
x 1	n 11	n 12		n 1 j		n 1 t	n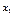
x 2	n 21	n 22		n 2 j		n 2 t	n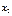
…
x i	ni 1	ni 2		nij		nit	n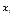
xs	ns 1	ns 2		nsj		nst	n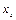
Всего	n	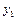n	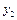…	n	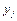…	n	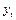n

Здесь частота n_ij показывает, что из n членов совокупности имеется n_ij таких, у которых переменная x принимает значения x_i, а переменная y – значения y_j.

Основными характеристиками корреляционной таблицы являются:

1. Общая средняя переменной X и переменной Y

;

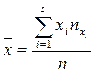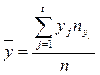
2. Дисперсия переменной X и переменной Y

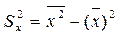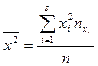
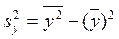, где

, где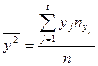

3. Групповые средние

, .

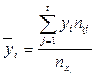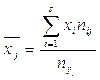Групповые средние называются также математическими ожиданиями: 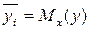– это математическое ожидание переменной Y, вычисленное в предположении, что переменная X приняла значение x; аналогично, .

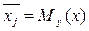Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием (групповой средней) другой. Корреляционная зависимость может быть представлена в виде

М_x (y)= f (x) (1) и M_y (x)=j(y) (2).

Уравнение (1) называется корреляционной зависимостью y на x; (2) – x на y. Эти уравнения называются также корреляционными уравнениями или уравнениями регрессии.

Для отыскания уравнения регрессии необходимо знать закон распределения двумерной случайной величины (X, Y). На практике исследователь располагает лишь выборкой пар значений (x_i, y_i) ограниченного объема. Поэтому можно говорить лишь об оценке (приближенном выражении) функций регрессии. Основными задачами регрессионного анализа являются:

1. установление формы и изучение зависимости между переменными, то есть вида функций (1) и (2). Предположение о виде этих функций можно сделать на основании эмпирических линий регрессии. Это ломаные, вершины которых находятся в точках (x_i, 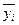) и (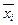, y_i) соответственно. Если обе функции линейные, то получим линейные корреляционные уравнения, а их графики называются прямыми регрессии.

2. оценка тесноты связи, то есть оценка степени рассеяния значений y около линии регрессии для разных значений x (или рассеяния значений x для разных значений y).

В случае линейной парной регрессии уравнения регрессии записываются в виде

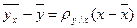и ,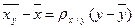

где 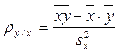; 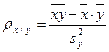– коэффициенты регрессии y на x и x на y соответственно.

Важным числовым показателем зависимости пары случайных величин является значение ковариации их совместного распределения, а точнее, коэффициент корреляции.

Ковариация двух случайных величин

cov (X, Y) = m =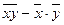

является величиной размерной, поэтому вместо нее обычно используют коэффициент корреляции. Коэффициент корреляции – это отношение ковариации к произведению средне квадратичных отклонений величин X и Y:

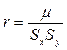
Коэффициент корреляции и коэффициенты регрессии взаимно связаны и взаимно выражаются друг через друга:

, ,

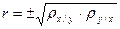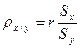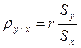
Коэффициент корреляции является показателем тесноты связи: чем ближе он к 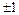, тем теснее связь, тем ближе значения Y расположены к прямой регрессии Y на X, а значения X к прямой X на Y. Коэффициент корреляции является показателем направления связи: если r >0, то связь между переменными прямая, то есть с увеличением одного фактора другой в среднем также увеличивается, если r <0, то связь между переменными обратная, то есть с увеличением одной переменной, другая в среднем уменьшается.

Упражнения.

9.1. Распределение 100 рабочих по стажу работы (X лет) и производительности труда (Y деталей/ч) дано в таблице:

Y X	5 – 10	10 - 15	15 - 20	20 – 25	25 - 30	Итого
1 – 3
3 – 5
5 – 7
7 – 9
9 – 11
Итого

Необходимо: 1) вычислить групповые средние и построить эмпирические линии регрессии; 2) найти уравнения прямых регрессии и построить их графики; 3) вычислить коэффициент корреляции; на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи между переменными X и Y; 4) оценить среднюю производительность рабочего со стажем 7 лет, используя соответствующие уравнения прямой регрессии.

9.2. Распределение 250 спортсменов по росту X(см) и весу Y(кг) дано в таблице:

Y X	60 – 70	70 – 80	80 - 90	90 – 100	100 - 110	Итого
165-170
170-175
175-180
180-185
185-190
190-195
Итого

Необходимо: 1) вычислить групповые средние и построить эмпирические линии регрессии; 2) найти уравнения прямых регрессии и построить их графики на том же чертеже; 3) вычислить коэффициент корреляции, на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи между переменными X и Y; 4) найти средний вес спортсмена ростом 180см, используя соответствующее уравнение регрессии.

9.3. Дано распределение 100 га земли по количеству внесенных удобрений X (ц/га) и по урожайности Y (ц/га):

Y X							Итого
Итого

Вычислить групповые средние и построить эмпирические линии регрессии; найти уравнения прямых регрессии и построить их графики на том же чертеже;

вычислить коэффициент корреляции, на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи; найти среднюю урожайность при внесении удобрений 20 ц/га.

9.4. Дано распределение 200 растений по массе каждого из них X(г) и по массе семян Y(г):

Y X						Итого
Итого

Найти групповые средние и построить групповые линии регрессии; вычислить коэффициент регрессии; вычислить коэффициент корреляции, решить вопрос о тесноте и направлении связи; составить уравнения прямых регрессии.

Варианты контрольных работ