Гомотетия как пример преобразования подобия

О п р е д е л е н и е. Подобием с коэффициентом называется преобразование плоскости, при котором все расстояния умножаются на .

Примеры подобий

1. Любое движение является подобием с коэффициентом .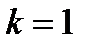

2. Гомотетией с центорм и коэффициентом называется отображение плоскости в себя, при котором каждой точке ставится в соответствие точка 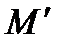такая, что .

Проверьте, что гомотетия является биективным отображением, а значит, является преобразованием плоскости.

Для любых двух точек и их образов при гомотетии имеем . Тогда и , то есть гомотетия с коэффициентом является подобием с коэффициентом .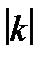

Из условия получаем формулы гомотетии

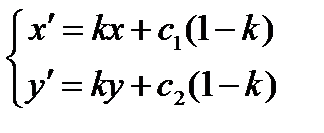позволяющие доказать свойства гомотетии:

a. При гомотетии прямая, не проходящая через центр гомотетии, переходит в параллельную ей прямую, а прямая, проходящая через центр гомотетии – в себя.

b. Гомотетия сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между» и отрезок переводит в отрезок, луч в луч, угол в угол.

c. Гомотетия переводит угол в равный угол (Почему?).

d. Гомотетия сохраняет ориентацию плоскости. Для доказательства этого свойства находим по формулам гомотетии координаты точек, определяющих репер – образ репера при гомотетии. Затем находим координаты базисных векторов репера и убеждаемся, что определитель матрицы перехода от базиса репера к базису репера равен , то есть реперы и одинаково ориентированы.

Свойства подобий

Т е о р е м а 1. (о разложении подобия в композицию гомотетии и движения) Всякое преобразование подобия можно представить как композицию гомотетии с тем же коэффициентом и движения.

Д о к а з а т е л ь с т в о. Пусть – подобие с коэффициентом . Если – гомотетия с коэффициентом , то – гомотетия с коэффициентом . Тогда композиция является движением и мы имеем – представление подобия в виде композиции гомотетии с тем же коэффициентом и движения.

Из этой теоремы и свойств гомотетии и движения получаем свойства подобий:

Подобие переводит прямую в прямую.
Подобие сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между» и отрезок переводит в отрезок, луч в луч, угол в угол, полуплоскость в полуплоскость.
Подобие переводит угол в равный угол.
Существуют подобия I и II рода.
Множество Р всех подобий плоскости является группой относительно композиции преобразований. Подгруппами этой группы являются: группа всех движений плоскости, множество всех гомотетий с общим центром, множество всех гомотетий и параллельных переносов.
Фигуры и называются подобными, если они эквивалентны относительно группы Р подобий. Примерами подобных фигур являются два треугольника, соответственные стороны которых пропорциональны, два эллипса (две гиперболы), эксцентриситеты которых равны, любые две параболы.