Движения плоскости, их свойства

Преобразование плоскости, сохраняющее расстояния, называется движением (перемещением) плоскости.

Примеры движений

1. Тождественное преобразование.

2. Параллельный перенос.

Параллельным переносом 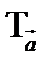на вектор 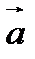называется отображение плоскости в себя, при котором каждой точке плоскости ставится в соответствие точка такая, что .

a) Отметим, что параллельный перенос определяется как отображение и, следовательно нужно доказать, что он является преобразованием плоскости, то есть проверить биективность отображения. Сделайте это самостоятельно.

b) Имеем . Тогда и , то есть параллельный перенос сохраняет расстояния, а значит, является движением плоскости.

3. Центральная симметрия.

Центральной симметрией относительно точки называется отображение плоскости в себя, при котором каждой точке плоскости ставится в соответствие точка такая, что .

a) Аналогично нужно показать, что центральная симметрия является преобразованием плоскости.

b) Из условий и получаем, что . Тогда , то есть центральная симметрия сохраняет расстояния, а значит, является движением плоскости.

Самостоятельно следует рассмотреть доказательство следующих важных теорем

Т е о р е м а 1. При движении образом репера является репер. Образом оротнормированного репера является ортонормированный репер.

Т е о р е м а 2. (о задании движения парой соответствующих ортонормированных реперов) Пусть и два ортонормированных репера. Существует единственное движение плоскости, которое репер переводит в репер . При этом движении каждая точка с координатами в репере переходит в точку с теми же координатами в репере .

Теоремы 1-2 позволяют доказать следующие свойства движений:

1. Движение переводит прямую в прямую, праллельные прямые в параллельные прямые.

2. Движение переводит полуплоскость в полуплоскость.

3. Движение сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между», поэтому переводит отрезок в отрезок, луч в луч, угол в угол.

4. Движение переводит угол в равный угол, перпендикулярные прямые в перпендикулярные прямые.

5. Любое движение либо сохраняет ориентацию плоскости (любой репер переводит в одинаково ориентированный с ним репер), либо меняет ориентацию плоскости (любой репер переводит в противоположно ориентированный с ним репер).
Отсюда имеем два вида движений: движения I рода (сохраняющие ориентацию плоскости) и движения II рода (меняющие ориентацию плоскости).

Формулы движений

Пусть – движение плоскости. Задав на плоскости прямоугольную систему координат , сможем найти формулы движения 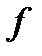– это формулы, выражающие координаты точки через координаты точки – прообраза точки .

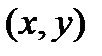Пусть при движении ортонормированный репер переходит в ортонормированный репер . Тогда по теореме 2 о задании движения парой ортонормированных реперов следует, что имеет координаты в репере .

Рассматривая и как старую и новую системы координат, получаем, что точка имеет соответственно старые координаты относительно репера 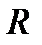и новые координаты относительно репера . Используя формулы преобразования координат при переходе от одной системы координат к другой, получим

(*),

где , если и одинаково ориентированы, то есть – движение первого рода, и , если и противоположно ориентированы, то есть – движение второго рода.

Формулы (*) это и есть формулы движения. Можно заметить, что матрица, составленная из коэффициентов при и 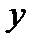в этих формулах, является ортогональной (сумма квадратов элементов одного и того же столбца равна 1, а сумма произведений соответствующих элементов разных столбцов равна 0); определитель этой матрицы равен 1 в случае движения первого рода и равен -1 в случае движения второго рода.

Имеет место следующая теорема

Т е о р е м а 3. (об аналитическом задании движения) Пусть – ортонормированный репер. Формулы

(**),

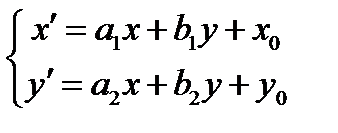где – ортогональная матрица, определяют движение первого рода, если определитель этой матрицы равен 1 и второго рода, если определитель этой матрицы равен -1.

При доказательстве этой теоремы следует обосновать три момента:

1. Формулы действительно задают преобразование плоскости (проверить биективность).

2. Преобразование сохраняет расстояния (вычисляя расстояние между точками и 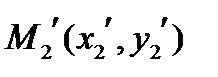, использовать формулы (**) и условие ортогональности матрицы, составленной из коэффициентов, показать, что ).

3. Показать, что реперы и одинаково ориентированы, то есть является движением первого рода, если и противоположно ориентированы, то есть – движение второго рода, если . Для этого, используя формулы (**) нужно найти координаты точек 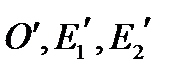образов точек , определяющих репер . Далее найти координаты векторов и и убедиться, что матрица перехода от базиса к базису имеет вид . Знак определителя этой матрицы характеризует одинаковость ориентации этих базисов, а значит и реперов и .

Примеры движений

У п р а ж н е н и е 1. Найти формулы параллельного переноса. Доказать, что праллельный перенос является движением первого рода. Определить неподвижные точки и неподвижные прямые при параллельном переносе. Доказать, что множество всех праллельных перносов является группой.

У п р а ж н е н и е 2. Поворотом плоскости вокруг точки на угол называется отображение плоскости в себя, при котором точка переходит сама в себя, любая другая точка плоскости переходит в точку такую, что расстояния и 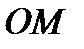равны и угол равен .

Задав на плоскости прямоугольную систему координат , выразите косинус и синус угла через косинусы и синусы углов и , образованных векторами и с вектором . Далее выразите косинусы и синусы углов и через координаты точек и . Убедитесь, что

, , где .

Решая систему относительно и , получим формулы поворота вокруг начала координат: .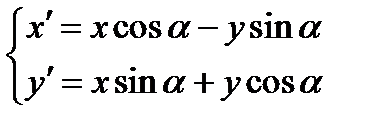

Убедитесь, что поворот вокруг точки является движением первого рода. Определите неподвижные точки при повороте. Выясните, что представляет собой поворот на угол . Докажите, что множество всех поворотов с общим центром является группой. Найдите формулы поворота вокруг точки .

У п р а ж н е н и е 3. Осевой с имметрией с осью называется отображение плоскости в себя, при котором каждой точке плоскости ставится в соответствие точка, симметричная ей относительно прямой .

Напомним, что каждая точка прямой симметрична сама себе. Точка, не лежащая на прямой , и симметричная ей точка определяют отрезок, перпендикулярный прмой , середина которого лежит на прямой .

Найдите формулы симметрии относительно оси 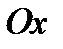, убедитесь, что осевая симметрия является примером движения второго рода. Найдите неподвижные точки, неподвижные прямые при осевой симметрии. Выясните, что представляет собой композиция двух осевых симметрий с параллельными осями, с пересекающимися осями.

У п р а ж н е н и е 4. Скользящей симметрией называется композиция осевой симметрии и параллельного переноса на вектор, параллельный оси симметрии: .