Группа преобразований плоскости

Пусть – множество всех преобразований плоскости. На этом множестве можно определить бинарную операцию – композицию преобразований: 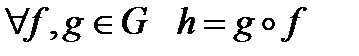– преобразование плоскости, представляющее собой последовательное выполнение преобразований и 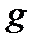(порядок выполнения преобразований в записи: справа налево).

Т е о р е м а. Множество всех преобразований плоскости является группой относительно композиции преобразований.

Пусть 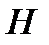некоторая подгруппа группы преобразований (вспомнить определение и признак подгруппы). Фигура называется эквивалентной фигуре относительно группы (), если существует преобразование такое, что . Можно показать, что эквивалентность фигур относительно группы преобразований является отношением эквивалентности.