Ответ 1: Лежат на одной или параллельных прямых
49. Указать необходимое и достаточное условие компланарности векторов  и
и 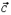 :
:
Ответ 1: 
50. Для векторного произведения векторов  и
и  справедливо свойство:
справедливо свойство:
Ответ 1: 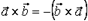
51. Смешанное произведение векторов 

Ответ 1: 
52. Указать необходимое и достаточное условие коллинеарности векторов  и
и 
Ответ 1: 
53. Расстояние между точками  и
и  определяется формулой:
определяется формулой:
Ответ 1: 
54. Указать необходимое и достаточное условие ортогональности векторов  и
и 
Ответ 1: 
55. Векторным произведением векторов  и
и  называется вектор, удовлетворяющий условиям
называется вектор, удовлетворяющий условиям
Ответ 1: 

 - правая тройка векторов
- правая тройка векторов
56. Скалярное произведение векторов  , т.е.
, т.е.  равно
равно
Ответ 1: 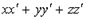
57. Скалярное произведение вектора 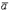 на сумму векторов
на сумму векторов  и
и  равно:
равно:
Ответ 1: 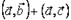
58. Скалярное произведение векторов  и
и  равно
равно
Ответ 1: 
59. Векторное произведение векторов  и
и  равно:
равно:
Ответ 1: 
60. Если векторы  не компланарны, то выполняется условием:
не компланарны, то выполняется условием:
Ответ 1: 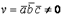
61. Если векторы  и
и  коллинеарны
коллинеарны  , тогда найдется число
, тогда найдется число  , удовлетворяющее:
, удовлетворяющее:
Ответ 1: 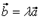
62. Произведением вектора  на число
на число  называется вектор
называется вектор 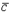 , удовлетворяющий условиям:
, удовлетворяющий условиям:
Ответ 1: 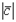 =
=  ,
, 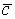 коллинеарен
коллинеарен  и направлен как
и направлен как 
63. Векторы  и
и  коллинеарны, если:
коллинеарны, если:
Ответ 1: 
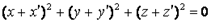
64. Решить систему уравнений: 
Ответ 1: 
65. Решить систему уравнений: 
Ответ 1: 
66. Решить систему уравнений: 
Ответ 1: 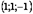
67. Решить систему уравнений: 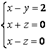
Ответ 1: 
68. Решить систему уравнений: 
Ответ 1: 
69. Решить систему уравнений: 
Ответ 1: 
70. Решить систему уравнений: 
Ответ 1: 
71. Решить систему уравнений: 
Ответ 1: 
72. Решить систему уравнений 
Ответ 1: 
73. Решить систему однородных уравнений 
Ответ 1: (0,0,0)
74. Найти  , если
, если  ;
; 
Ответ 1: 
75. Найти  , если
, если  ;
; 
Ответ 1: 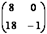
76. Найти  , если
, если  ;
; 
Ответ 1: 
77. Найти  , если
, если  ;
; 
Ответ 1: 
78. Найти  , если
, если  ;
; 
Ответ 1: 
79. Найти  , если
, если  ;
; 
Ответ 1: 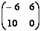
80. Найти  , если
, если  ;
; 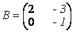
Ответ 1: 
81. Найти  , если
, если  ; и
; и 
Ответ 1: 
82. Найти  , если
, если  и
и 
Ответ 1: 
83. Найти  , если
, если  ;
; 
Ответ 1: 
84. Вычислить 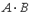 , если
, если  ;
; 
Ответ 1: 
85. Найти ранг матрицы 
Ответ 1: 2
86. Найти обратную матрицу  , если
, если 
Ответ 1: 
87. Найти ранг матрицы 
Ответ 1: 2
88. Найти произведение матриц  и
и 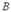 , если
, если  .
.
Ответ 1: 
89. Найти алгебраическое дополнение  определителя
определителя 
Ответ 1: 12
90. Найти алгебраическое дополнение 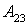 определителя
определителя 
Ответ 1: 10
91. Найти алгебраическое дополнение  определителя
определителя 
Ответ 1: -4
92. Найти алгебраическое дополнение  определителя
определителя 
Ответ 1: -12
93. Найти алгебраическое дополнение 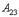 определителя
определителя 
Ответ 1: -20
94. Решить неравенство: 
Ответ 1: 
95. Решить уравнение: 
Ответ 1: -1
96. Решить уравнение: 
Ответ 1: -6
97. Вычислить: 
Ответ 1: -5
98. Вычислить: 
Ответ 1: -11
99. Вычислить: 
Ответ 1: 19
100. Вычислить: 
Ответ 1: 6
101. Сложение матриц А размерности  и В размерности
и В размерности 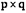 возможно, если
возможно, если
Ответ 1: 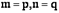
102. Матрицы 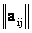 размерности
размерности  и
и  размерности
размерности  называются равными, если
называются равными, если
Ответ 1: 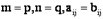
 2015-10-22
2015-10-22 1301
1301








