2015-10-22
978
-
, где 
обозначает определитель. -
для любых двух обратимых матриц 
и 
. -
, где 
обозначает транспонированную матрицу. -
для любого коэффициента 
. -
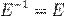. - Если необходимо решить систему линейных уравнений
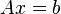, (b — ненулевой вектор) где 
— искомый вектор, и если 
существует, то 
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц 
(трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
.
Вторая матрица после применения всех операций станет равна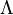 
, то есть будет искомой. Сложность алгоритма — 
.
