Определение определителя и его основные свойства

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ.

Действия над матрицами

1. Сложение матриц

Суммой двух матриц A = (aij) и B = (bij) одинакового размера называется такая матрица C = (cij) того же размера, что cij = aij + bij

Свойства сложения матриц

1) Ассоциативность.

Для любых матриц A,B и C одинакового размера выполнено равенство (A + B) + C = A + (B + C).

2) Коммутативность.

Для любых матриц A и B одинакового размера выполнено A+B = B+A.

3) Нулевая матрица.

Матрица O произвольного размера k×n, все элементы которой равны нулю, называется нулевой матрицей. Для любой матрицы A размера k×n выполнено следующее равенство A + O = A.

4) Противоположная матрица.

Для любой матрицы A размера k×n существует матрица B размера k × n такая, что A + B = O. Матрица B называется противоположной к A и обозначается -A.

2. Умножение матрицы на число

Всякую матрицу A можно умножить на число α, для этого каждый элемент матрицы A нужно умножить на α.

Свойства умножения матрицы на число

1) Ассоциативность.

Для любой матрицы A и чисел α, β выполнено (αβ)A = α(βA).

2) Дистрибутивность.

2.1) Для любой матрицы A и чисел α, β выполнено (α+ β)A = αA + βA.

2.2) Для любых двух матриц A и B одинакового размера и числа α выполнено α(A + B) =αA + αB.

3. Умножение матриц

Умножение матриц A размера k×n и B размера s×m определено, если число столбцов матрицы A равно числу строк матрицы B, то есть n = s. Результат умножения AB есть матрица C = (cij)

размера k×m, для которой cij = ai1b1j + ai2b2j + … + ainbnj

Свойства умножения матриц

1) Не коммутативность.

Произведение матриц в общем случае не коммутативно, то есть существуют матрицы A и B, что A • B ≠ B • A.

2) Ассоциативность.

Для любых трех матриц A, B и C подходящего размера выполнено (A • B) •C = A • (B • C).

3) Единичная матрица.

Квадратная матрица En = 1 0 … 0

0 1 … 0

……….

0 0 … 1

размера n×n называется единичной. Для любых матриц A размера k×n и B размера n×m

выполнены равенства: A•En = A, En•B = B:

4) Дистрибутивность.

4.1) Для любых трёх матриц A, B и C подходящего размера выполнено равенство A • (B + C) = A • B + A • C.

4.2) Для любых трёх матриц A, B и C подходящего размера выполнено равенство

(A + B) • C = A•C + B • C

Определение определителя и его основные свойства

Определителем квадратной матрицы A = (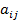) размера n £ n называется алгебраическая сумма всевозможных произведений элементов 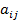, взятых по одному из каждой строки и каждого столбца матрицы A. В каждом произведении сомножители записываются в порядке следования строк, а номера столбцов образуют перестановку (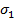; ;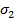:::; 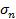) принадлежит Sn. Всего под знаком суммы стоит n! слагаемых; слагаемые, отвечающие четным перестановкам, входят со знаком плюс, а, отвечающие нечетным перестановкам — со знаком минус

Свойства:

1. Определители любой квадратной матрицы A и транспонированной с ней матрицы 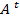совпадают.

2. При перестановке местами любых двух строк матрицы определитель меняет знак на противоположный

3. Если элементы какой-либо строки представлены в виде суммы двух строк, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны первым слагаемым, во второй — вторым

a11 a12 … a1n a11 a12 … a1n a11 a12 … a1n

……………………………….. ……………… ………………

bi1 + ci1 bi2 + ci2::: bin + cin = bi1 bi2::: bin + ci1 ci2 … cin

……………………………….. …………….... ………………

an1 an2 … ann an1 an2::: ann an1 an2 … ann

4. Если все элементы некоторой строки определителя имеют общий множитель, то этот множитель можно вынести за знак определителя.

5. Если в квадратной матрице две строки совпадают, то ее определитель равен нулю.

6. Определитель матрицы, содержащей строку нулей, равен нулю.

7. Определитель матрицы не изменится если к одной ее строке прибавить другую ее строку, умноженную на любое число.