Та особливості виконання арифметичних операцій
Співпроцесор майже завжди виконує всі операції у форматі long double. Він має спеціальний керуючий двобайтовий регістр. Установлення окремих бітів регістра диктує співпроцесору ту чи іншу поведінку. Його біти відповідають за те, як будуть округлятися числа, як співпроцесор розуміє нескінченність. Розглянемо тільки два біти регістра – восьмий і дев'ятий. Саме вони визначають, як оброблятимуться числа всередині співпроцесора.
Якщо восьмий біт містить одиницю (так установлено за умовчанням), то 10 байтів внутрішніх регістрів співпроцесора використовуватимуться повністю, і ми одержимо повноцінний long double. Якщо ж цей біт дорівнює нулю, то все визначається значенням дев'ятого біта. Якщо він дорівнює одиниці, то використовуються 53 розряди мантиси (інші завжди дорівнюють нулю). Якщо ж цей біт дорівнює нулю – то лише 24 розряди мантиси. Це збільшує швидкість обчислень, але зменшує точність. Іншими словами, точність роботи співпроцесора може бути знижена до типу double чи навіть float. Однак це стосується тільки мантиси, порядок завжди буде містити 15 бітів, так що діапазон типу long double зберігається в будь-якому випадку.
Сучасні співпроцесори обробляють числа з такою швидкістю, що навряд чи в кого-небудь може виникнути необхідність у прискоренні за рахунок точності. Проте це треба знати.
Ми вже зазначали, що властивість повноти не виконується при машинному зображенні дійсних чисел, оскількине кожен правильний дріб може бути зображений у вигляді скінченного. Наприклад, 1/9 = 0.11111..., 1/3 = 0.333333... і т. д. При роботі з такими числами використовується не точне, а наближене значення. Це потрібно враховувати при написанні програм.
Двійкові дроби теж можуть бути нескінченними. Більше того, не кожне число, що виражається скінченним десятковим дробом, може бути також зображено скінченним двійковим. Наприклад, число 1/5 зображується скінченним десятковим дробом як 0.2, але воно не може бути виражене скінченним двійковим дробом. Такі дроби завжди періодичні, оскільки раціональне число зображується скінченним або періодичним дробом у системі числення з будь-якою основою.
Розглянемо кілька прикладів некоректного використання дійсних типів.
1. Приклад появи зайвих цифр.
#include <string.h>
#include <stdlib.h>
Main()
{
float r;
r=0.1;
printf("%.15e",r);
}
Після виконання програми ми побачимо 1.00000001490116e–001. Точність типу float – 7–8 десяткових розрядів, так що результат правильний. Однак звідки взялися інші цифри?
Виявляється, число 0.1 не зображується у вигляді скінченного двійкового дробу, воно дорівнює 0.0(0011). І цей нескінченний двійковий дріб округляється на 24 знаках; ми одержуємо не 0.1, а деяке наближене число. Проекспериментувавши з різними числами, можна помітити, що точно зображуються ті числа, що виражаються у вигляді 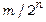 , де
, де 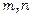 – деякі цілі числа.
– деякі цілі числа.
2. Приклад незрозумілого результату виконання програми.
#include <string.h>
Main()
{
float r;
r=0.1;
if (r==0.1)
printf("дорівнює \n");
Else
printf("не дорівнює \n");
}
Після запуску програми ми отримаємо "не дорівнює". Змінна r при присвоюванні одержує значення 0.100000001490116, тому що спочатку число 0.1 перетворюється до типу long double, а потім, при присвоюванні, відбувається округлення до типу float. Процесори Intel працюють із 10-байтним типом long double, тому й ліва, і права частини рівності в умові спочатку перетворюються на цей тип, і лише потім здійснюється порівняння. Число, що зберігається в змінній r (уже не 0.1!), зображується у вигляді скінченного двійкового дробу. При перетворенні цього числа в long double молодші, надлишкові, порівняно з типом float, розряди мантиси, просто заповнюються нулями. Ми одержуємо те саме число, тільки записане у форматі long double.
Число 0.1 із правої частини рівності перетвориться в long double без проміжного перетворення в single і матиме нескінченне зображення у двійковому коді, а деякі з молодших розрядів мантиси міститимуть ненульові значення. Тому порівнюють близькі, але не рівні числа.
Якщо замінити число 0.1 на 0.5, то одержимо "дорівнює", тому що 0.5 – це скінченний двійковий дріб. При прямому зведенні його до типу extended у молодших розрядах будуть нулі. Такі самі нулі виявляються в цих розрядах при перетворенні числа 0.5 типу float у тип long double. Тому в результаті ми порівнюємо два однакових числа.
3. Розглянемо програму:
#include <string.h>
#include <stdlib.h>
Main()
{
float r1;
double r2;
r1=0.1;
r2=0.1;
if (r1==r2)
printf("дорівнює");
Else
printf("не дорівнює");
}
Одержимо такий самий результат, тобто "не дорівнює", із тих самих причин.
4. Розглянемо програму:
#include <stdio.h>
Main()
{
float r;
int i;
r=1;
for(i=1;i<=10;i++)
r-=0.1;
printf("r=%e\n",r);
}
Після виконання програми на екрані з'явиться –7.301569E–008, тому що число 0.1 не може бути передане точно у жодному із дійсних типів. При цьому постійно відбуваються округлення, завдяки яким ми одержуємо в результаті не нуль, а майже нуль.
Коли ми маємо справу з обчисленнями з обмеженою точністю, виникає парадокс. Наприклад, ми маємо точність до трьох значущих цифр. Додамо до числа 1.00 число 1.00*10–4. Ми мали б одержати 1.0001. Однак у нас обмежена точність, тому ми змушені округляти до трьох значущих цифр. У результаті виходить 1.00. Іншими словами, до деякого числа ми додаємо інше, яке більше нуля, і, через обмежену точність, одержуємо те саме число.
Означення 5.2. Найменше додатне число, при додаванні якого до одиниці результат не дорівнює одиниці, називається машинним епсілоном.
Написати програму для обчислення машинного епсілона.
#include <stdio.h>
Main()
{
double r;
r=1;
while (1+r/2>1) r=r/2;
printf("%.20e",r);
}
У результаті буде отримане число 1.08420217248550e–19 для комп'ютерів класу Pentium III.
Завдання для самостійної роботи
1. Перевести десяткові числа у двійкові, вісімкові та шістнадцяткові:
а) 3.8;
б) 17.0162;
в) 0.313;
г) 7.127;
д) 13.0015.
2. Перевести шістнадцяткові числа в десяткові, двійкові, вісімкові:
а) AC2F.F;
б) FF.F;
в) A3B.12.
3. Перевести двійкове число у вісімкове та шістнадцяткове:
а) 10011011.1101;
б) 101011100.001101;
в) 1110001.010101.
4. Перевести число з десяткової у двійкову систему числення.
5. Перевести число із двійкової в десяткову систему числення.
6. Обчислити вирази:
Адитивні операції:
а) 11001 + 101;
б) 11001 + 11001;
в) 1001 – 111;
г) 10011 + 101;
д) 11011 – 1111;
е) 11111 + 10011.
Мультиплікативні операції:
а) 1101 / 110;
б) 1010 / 10;
в) 1011 / 11;
г) 101011 / 101;
д) 10010 / 1001.
е) 1101 * 1110;
є) 1010 * 110;
ж) 1011 * 11;
з) 101011 * 1101;
и) 10010 * 1001.
7. Надрукувати число х таке, що 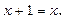
8. Надрукувати ціле число х таке, що 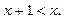
РЕАЛІЗАЦІЯ КОНЦЕПЦІЇ
 2015-10-22
2015-10-22 477
477








