Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов 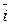, 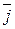и :

Пусть заданы два вектора 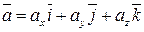и . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойствам векторного произведения):

,

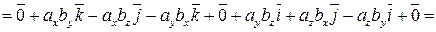
т.е.

. (8)

Полученную формулу можно записать еще короче:

, (9)

так как правая часть равенства (8) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (9) легко запоминается.

. Некоторые приложения векторного произведения

Установление коллинеарности векторов

Если , то (и наоборот), т.е.

.

Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов и , т.е. . И, значит, .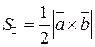

Определение момента силы относительно точки

Пусть в точке приложена сила и пусть 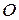- некоторая точка пространства.

Из физики известно, что моментом силы относительно точки 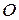называется вектор , который проходит через точку 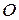и:

1) перпендикулярен плоскости, проходящей через точки , , ;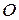

2) численно равен произведению силы на плечо

;

3) образует правую тройку с векторами и .

Стало быть, .

Нахождение линейной скорости вращения

Скорость точки твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется формулой Эйлера 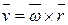, где , где 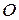- некоторая неподвижная точка оси.