Системы 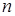и определители высших порядков

Систему линейных уравнений с 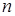неизвестными можно записать в таком виде:

Для этого случая также можно составить главный и вспомогательные определители, а неизвестные определять по правилу Крамера. Проблема состоит в том, что определители более высокого порядка могут быть вычислены только путем понижения порядка и сведения их к определителям третьего порядка. Это может быть осуществлено способом прямого разложения по элементам строк или столбцов, а также с помощью предварительных элементарных преобразований и дальнейшего разложения.

Пример 4. Вычислить определитель четвертого порядка

Решение найдем двумя способами:

а) путем прямого разложения по элементам первой строки:

б) путем предварительных преобразований и дальнейшего разложения

	а) из І строки вычтем ІІІ
б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

Пример 5. Вычислить определитель пятого порядка, получая нули в третьей строке с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

из второго столбца вычтем третий:

из второй строки вычтем третью:

Пример 6. Решить систему:

Решение. Составим определитель системы и, применив свойства определителей, вычислим его:

(из первой строки вычтем третью, а затем в полученном определителе третьего порядка из третьего столбца вычитаем первый, умноженный на 2). Определитель , следовательно, формулы Крамера применимы.

Вычислим остальные определители:

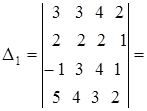
Четвертый столбец умножили на 2 и вычли из остальных

Четвертый столбец вычли из первого, а затем, умножив на 2, вычли из второго и третьего столбцов.

.

Здесь выполнили те же преобразования, что и для .

.

При нахождении первый столбец умножили на 2 и вычли из остальных.

По правилу Крамера имеем:

.

После подстановки в уравнения найденных значений убеждаемся в правильности решения системы.

2. МАТРИЦЫ и ИХ ИСПОЛЬЗОВАНИЕ

В РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Понятие о матрицах

Матрицей называется прямоугольная таблица чисел следующего вида:

- элемент матрицы

(первый индекс – это номер строки, второй индекс – это номер столбца ; ). Размерность данной матрицы , а в общем виде – .

Матрица – это таблица и вычислить ее нельзя. Например, запасы тканей на конец года на базах Облпотребсоюза представлены в табл. 1.

Таблица 1. Запасы тканей на базах (тыс. грн.)

Базы Вид ткани	Донецкая	Артемовская	Мариупольская	Дружковская
Хлопчатобумажные	120,8	110,0	185,7	84,2
Шерстяные	41,3	13,0	60,0	18,4
Шелковые (натуральные)	15,7			12,3
Шелковые (искусственные)	21,8	12,0	40,0	15,0
Льняные	13,2	16,0	32,3	20,0

Здесь мы имеем матрицу размерности .

Матрица называется квадратной, если число строк равно числу столбцов (порядок матрицы). Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Если в матрице поменять местами строки и столбцы, то эта операция называется транспонированием.

.

Матрица, все элементы которой равны 0, называется нуль - матрицей.

Квадратная матрица, у которой отличны от нуля лишь диагональные элементы, называется диагональной ( – диагональная матрица IV порядка).

.

Квадратная матрица называется единичной, если элементы главной диагонали равны 1, а все остальные – нули (это матрица ). Матрицы одной размерности считаются равными, если у них совпадают соответствующие элементы. Каждой квадратной матрице можно поставить в соответствие определитель. Если определитель матрицы равен 0, то она называется вырожденной, если определитель не равен 0, то матрица – невырожденная.