Первичная обработка статистических данных

Математическая статистика – это наука о методах сбора, обработки, представления, анализа и интерпретации наблюдений массовых случайных явлений, обладающих статистической устойчивостью с целью выявления закономерностей. Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующие эти объекты. Для изучения выбранных объектов проводят наблюдения. Различают сплошное и выборочное наблюдения. При сплошном наблюдении обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяется крайне редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование практически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Различают следующие типы отборов:

Простым случайным называют такой, отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами: жеребьевкой; по таблице случайных чисел. Если выбранные объекты не возвращаются в генеральную совокупность, то выборка является простой случайной бесповторной. Типическим называют отбор, при котором объекты отбираются не извсей генеральной совокупности, а из каждой ее «типической части». Например, пусть некоторое объединение шахт исследует вопрос надежности работы определенного оборудования. Тогда отбор показателей производят не извсей совокупности, а по каждой шахте в отдельности. Типическим отборомпользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если в объеди-

нении имеются шахты с различными горно-геологическими условиями, то здесь типический отбор целесообразен. Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 10% перфораторов для выборочного контроля изношенно-

сти, то отбирают каждый десятый. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно. На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты. При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен или не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект не возвращается в генеральную совокупность.

Проверка данных может осуществляться на многих этапах статистических исследований:

• по корреляционному полю до первичной обработки данных при двумерном статистическом анализе;

• по статистическому ряду при одномерном анализе;

• по закону распределения при одномерном анализе.

Для проверки по корреляционному полю случайных величин Х и У, не разбитых на дискретные категории, необходимо построить точки в прямоугольной системе координат (х₁;y₁), (х₂;y₂),..., (х_i;y_i), …, (х_n;y_n). Полученное поле точек (диаграмма рассеяния) позволяет определить грубые ошибки и выбросы, не замеченные одномерным анализом каждой из переменных.

Исходные данные:

№	Y	X₁	X₂
		1,09	0,031
		4,99	0,042
		1,69	0,046
		5,15	0,033
		0,93	0,03
		5,04	0,024
		0,86	0,07
		4,97	0,03
		0,99	0,03
		5,05	0,051
		4,87	0,014
		2,11	0,03
		5,48	0,04
		1,21	0,048
			0,078
		0,84	0,063
		4,76	0,047
		1,16	0,033
		5,23	0,076
		1,36	0,053
		1,18	0,08
		5,26	0,059
		0,81	0,027
		5,33	0,035
		2,01	0,039
		5,12	0,062
		1,09	0,051
		5,01	0,05
		1,37	0,027
		4,78	0,033

№	Y	X₁	X₂
		4,8	0,047
		4,79	0,049
		5,13	0,032
		1,91	0,062
		5,24	0,054
		1,02	0,082
		4,9	0,054
		1,71	0,059
		5,26	0,063
		0,82	0,034
		4,96	0,038
		1,05	0,045
		5,83	0,02
		1,54	0,032
		5,27	0,059
		1,12	0,066
		5,34	0,023
		1,17	0,039
		5,42	0,052
		1,52	0,089
		1,23	0,029
		4,95	0,022
		1,28	0,062
		5,32	0,063
		0,55	0,047
		4,85	0,026
		1,08	0,047
		5,01	0,037
		0,94	0,025
		5,28	0,029

№	Y	X₁	X₂
		4,85	0,023
		0,63	0,025
		4,82	0,038
		1,22	0,036
		5,05	0,035
		1,26	0,042
		5,18	0,052
		1,06	0,053
		4,73	0,038
		1,33	0,059

№	Y	X₁	X₂
		0,85	0,037
		5,45	0,052
		0,93	0,035
		4,58	0,022
		1,25	0,078
		5,31	0,065
		1,12	0,04
		4,74	0,028
		0,98	0,045
		0,98	0,075

Для признака Х₁ определим наибольшее и наименьшее значение:

Х_min = 0,55

X_max = 6

объем выборки n = 80

Число рациональных интервалов определим с помощью формулы Стерджесса:

k = 1 + 3,332 lg n = 1 + 1,332 lg 80 = 7,3221

Определим шаг интервала:

h = (X_max – X_min) / k = (6 – 0,55) / 7,3221 = 0,7443

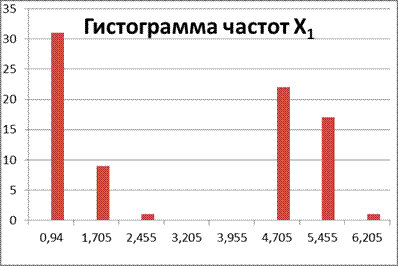
Произведем группировку данных для признака Х₁. Для этого подсчитаем, сколько значений признака Х₁ попадет в каждый из интервалов разбиения. Причем, при совпадении значения признака с одной из границ интервала, включаем это значение в левый интервал. Результаты группировки заносим в таблицу:

Интервал лев.	0,55	1,33	2,08	2,83	3,58	4,33	5,08	5,83
Интервал прав.	1,33	2,08	2,83	3,58	4,33	5,08	5,83	6,58
Середина интервала	0,94	1,705	2,455	3,205	3,955	4,705	5,455	6,205
Частота

Проверка: 31+9+1+22+17+1=80 => верно.

Для признака Х₂ определим наибольшее и наименьшее значение:

Х_min = 0,014

X_max = 0,3

объем выборки n = 80

Число рациональных интервалов определим с помощью формулы Стерджесса:

k = 1 + 3,332 lg n = 1 + 1,332 lg 80 = 7,3221

Определим шаг интервала:

h = (X_max – X_min) / k = (0,014 – 0,3) / 7,3221 = 0,03906

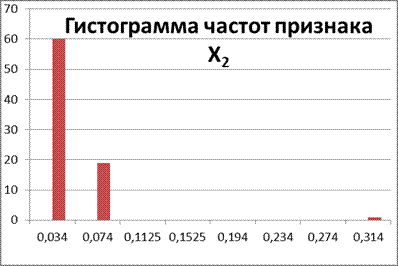
Произведем группировку данных для признака Х₂. Для этого подсчитаем, сколько значений признака Х₂ попадет в каждый из интервалов разбиения. Причем, при совпадении значения признака с одной из границ интервала, включаем это значение в левый интервал. Результаты группировки заносим в таблицу:

Интервал лев.	0,014	0,054	0,094	0,131	0,174	0,214	0,254	0,294
Интервал прав.	0,054	0,094	0,131	0,174	0,214	0,254	0,294	0,334
Середина интервала	0,034	0,074	0,1125	0,1525	0,194	0,234	0,274	0,314
Частота

Проверка: 60+19+1=80 => верно.

Для признака Y определим наибольшее и наименьшее значение:

Х_min = 60

X_max = 255

объем выборки n = 80

Число рациональных интервалов определим с помощью формулы Стерджесса:

k = 1 + 3,332 lg n = 1 + 1,332 lg 80 = 7,3221

Определим шаг интервала:

h = (X_max – X_min) / k = (266 – 60) / 7,3221 = 26,623

Произведем группировку данных для признака Y. Для этого подсчитаем, сколько значений признака Y попадет в каждый из интервалов разбиения. Причем, при совпадении значения признака с одной из границ интервала, включаем это значение в левый интервал. Результаты группировки заносим в таблицу:

Интервал лев.
Интервал прав.
Середина интервала	73,5	100,5	127,5	154,5	181,5	208,5	235,5	262,5
Частота

Графически статистические данные представляем гистограммой и полигоном относительных частот. При построении гистограммы на оси абсцисс откладывают интервалы разбиения признака Х, при построении полигона – середины интервалов разбиения признака х_i. По оси ординат в каждом случае откладывают ординаты w_i/h.. Полученную ступенчатую фигуру называют гистограммой, ломаную линию – полигоном.