Гипотеза – это высказывание предположительного характера. Под статистической гипотезой понимают гипотезу о параметрах распределения или виде функции распределения генеральной совокупности. Примерами статистических гипотез являются следующие высказывания: генеральная совокупность, имеет нормальный закон распределения или генеральная средняя. Нулевой гипотезой называют основную гипотезу и обозначают символом Но. Обычно нулевые гипотезы утверждают, что различие между сравниваемыми величинами (параметрами или функциями распределения) отсутствуют, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки. Альтернативной (конкурирующей) называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная, которую обозначают символом Н1. Проверку статистических гипотез обычно осуществляют в следующем порядке:
А) Располагая выборочными данными х1, х2, …, х и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Н0, которую называют основной или нулевой, и конкурирующую гипотезу Н1. Конкурирующая гипотеза представляет собой ту гипотезу, которая будет принята, если отвергнут основную гипотезу.
Б) Задаются вероятностью α, которую называют уровнем значимости ошибки первого рода. Поясним ее смысл. Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным, т.е. по ограниченному ряду наблюдений, следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов: отвергают гипотезу Н0, или, иначе, принимают альтернативную гипотезу Н1, тогда как на самом деле гипотеза Н0 верна – это ошибка первого рода; принимают гипотезу Н0, тогда как на самом деле высказывание Н0 неверно, т.е. верной является гипотеза Н1 – это ошибка второго рода. Значит, уровень значимости α - это вероятность ошибки первого рода, то есть вероятность того, что верная основная гипотеза будет отвергнута и принята ошибочная конкурирующая гипотеза.
В) Вводят статистический критерий проверки сформулированных гипотез, который представляет собой случайную величину, подчиняющуюся определенному заранее известному закону распределения, если верна основная гипотеза. По уровню значимости ошибки первого рода строят допустимую область (где принимается гипотеза Н0) и критическую область где отвергается гипотеза Н0 и принимается гипотеза Н1).
Г) По результатам выборки вычисляют наблюдаемое значение критерия и определяют область, в которую полученное значение критерия попадает. Если наблюдаемое значение критерия попало в критическую область, то гипотезу Н0 отвергают и принимают гипотезу Н1. Если наблюдаемое значение критерия попало в допустимую область, то говорят, что нет оснований отвергнуть гипотезу Н0.
Требуется при заданном уровне значимости α проверить, подчиняется ли генеральная совокупность выбранному теоретическому закону распределения f(x).
Выдвинем гипотезы
Н0: Признак Х1 подчиняется закону распределения f(x)
Н1: Признак Х1не подчиняется закону распределения f(x)
Для проверки сформулированных гипотез при помощи критерия Пирсона необходимо выполнить ряд расчетов.
Для каждого интервала признака Х1 необходимо вычислить вероятности по-
падания признака в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально:
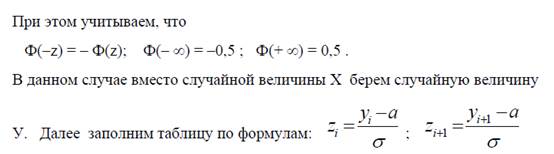

причем крайнюю левую точку интервала заменяем на – ∞; крайнюю правую точку заменяем на + ∞, поскольку теоретическое нормальное распределение определено на всей числовой оси.
| xi | xi+1 | ni | zi | zi+1 | Ф(zi) | Ф(zi+1) | ni* | Ni* | Ni | Bi | Vi | P |
| 0,55 | 1,33 | -1,45 | -1,01 | -0,5 | -0,343 | 12,56 | 12,56 | 27,07274 | 76,5127 | 0,156963 | ||
| 1,33 | 2,08 | -1,01 | -0,58 | -0,343 | -0,2202 | 9,831 | 47,782 | 29,87509 | 2,09283 | 0,122886 | ||
| 2,08 | 2,83 | -0,58 | -0,16 | -0,22 | -0,0634 | 12,54 | 0,156764 | |||||
| 2,83 | 3,58 | -0,16 | 0,264 | -0,063 | 0,10418 | 13,4 | 0,167561 | |||||
| 3,58 | 4,33 | 0,26 | 0,688 | 0,1042 | 0,25424 | 12,01 | 0,150066 | |||||
| 4,33 | 5,08 | 0,69 | 1,112 | 0,2542 | 0,36685 | 9,009 | 9,009 | 18,73305 | 53,7241 | 0,112609 | ||
| 5,08 | 5,83 | 1,11 | 1,535 | 0,3669 | 0,43765 | 5,664 | 10,652 | 3,783148 | 27,1312 | 0,070801 | ||
| 5,83 | 6,58 | 1,54 | 1,959 | 0,4377 | 0,5 | 4,988 | 0,062348 | |||||
| 79,46403 | 159,464 |
После заполнения 3–го столбца отмечаем, что 4 элемента в этом столбце меньше пяти. Поскольку в критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты. Делаем проверку:
80+79,46403=159,464 => верно
Запишем наблюдаемое значение критерия: χ2набл = 79,46403. Выберем уровень значимости ошибки α=0,05. Число степеней свободы равно k = m –2 – 1, где m – число интервалов после объединения. В нашем случае число интервалов после объединения m = 4. Тогда число степеней свободы равно k = 4 – 3 = 1. По таблице критических точек χ2 (Приложение 5) находим χ2кр (0,05; 1) = 3,84. Сравниваем: χ2набл > χ2кр. Следовательно, есть основания отвергнуть гипотезу о нормальном законе распределения признака Х1 и принять гипотезу Н1.
Выдвинем гипотезы
Н0: Признак Х2 подчиняется закону распределения f(x)
Н1: Признак Х2не подчиняется закону распределения f(x)
Для проверки сформулированных гипотез при помощи критерия Пирсона необходимо выполнить ряд расчетов.
Для каждого интервала признака Х2 необходимо вычислить вероятности по-
падания признака в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально:


причем крайнюю левую точку интервала заменяем на – ∞; крайнюю правую точку заменяем на + ∞, поскольку теоретическое нормальное распределение определено на всей числовой оси.
| xi | xi+1 | ni | zi | zi+1 | Ф(zi) | Ф(zi+1) | ni* | Ni* | Ni | Bi | Vi | P |
| 0,014 | 0,054 | -0,15 | 0,027 | -0,5 | 0,01088 | 40,87 | 40,87 | 8,954169 | 88,0842 | 0,510879 | ||
| 0,054 | 0,094 | 0,03 | 0,209 | 0,0109 | 0,08281 | 5,755 | 39,13 | 9,352106 | 10,2224 | 0,071932 | ||
| 0,094 | 0,131 | 0,21 | 0,377 | 0,0828 | 0,14701 | 5,136 | 0,064203 | |||||
| 0,131 | 0,174 | 0,38 | 0,573 | 0,147 | 0,21659 | 5,566 | 0,069571 | |||||
| 0,174 | 0,214 | 0,57 | 0,755 | 0,2166 | 0,27474 | 4,652 | 0,058154 | |||||
| 0,214 | 0,254 | 0,75 | 0,936 | 0,2747 | 0,32546 | 4,057 | 0,050718 | |||||
| 0,254 | 0,294 | 0,94 | 1,118 | 0,3255 | 0,36826 | 3,424 | 0,042798 | |||||
| 0,294 | 0,334 | 1,12 | 1,3 | 0,3683 | 0,5 | 10,54 | 0,131745 | |||||
| 18,30627 | 98,3066 |
После заполнения 3–го столбца отмечаем, что 6 элементов этом столбце меньше пяти. Поскольку в критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты. Делаем проверку:
80+18,30627=98,3066 => верно
Запишем наблюдаемое значение критерия: χ2набл = 18,30627. Выберем уровень значимости ошибки α=0,05. Число степеней свободы равно k = m –2 – 1, где m – число интервалов после объединения. В нашем случае число интервалов после объединения m = 2. Тогда число степеней свободы равно k = 2 – 3 = -1. По таблице критических точек χ2 (Приложение 5) находим χ2кр (0,05; -1) – не существует. Следовательно, есть основания отвергнуть гипотезу о нормальном законе распределения признака Х2 и принять гипотезу Н1.
Выдвинем гипотезы
Н0: Признак У подчиняется закону распределения f(x)
Н1: Признак У не подчиняется закону распределения f(x)
Для проверки сформулированных гипотез при помощи критерия Пирсона необходимо выполнить ряд расчетов.
Для каждого интервала признака У необходимо вычислить вероятности попадания признака в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально:


причем крайнюю левую точку интервала заменяем на – ∞; крайнюю правую точку заменяем на + ∞, поскольку теоретическое нормальное распределение определено на всей числовой оси.
| yi | yi+1 | ni | zi | zi+1 | Ф(zi) | Ф(zi+1) | ni* | Ni* | Ni | Bi | Vi | P |
| -6,14 | -3,79 | -0,5 | -0,4999 | 0,006 | 0,006 | 53964,01 | 7,57E-05 | |||||
| -3,79 | -1,44 | -0,5 | -0,4252 | 5,981 | 5,981 | 16,78321 | 42,8022 | 0,074763 | ||||
| -1,44 | 0,907 | -0,425 | 0,31789 | 59,44 | 59,44 | 27,51335 | 6,07335 | 0,743052 | ||||
| 0,91 | 3,255 | 0,3179 | 0,49943 | 14,52 | 14,52 | 0,181543 | ||||||
| 3,26 | 5,603 | 0,4994 | 0,5 | 0,045 | 0,045 | 0,000566 | ||||||
| 5,6 | 7,951 | 0,5 | 0,5 | 8E-07 | 8E-07 | 1,05E-08 | ||||||
| 7,95 | 10,3 | 0,5 | 0,5 | 7E-14 | 8,88E-16 | |||||||
| 10,3 | 12,65 | 0,5 | 0,5 | |||||||||
| 54008,3 | 54088,3 |
После заполнения 3–го столбца отмечаем, что 6 элементов этом столбце меньше пяти. Поскольку в критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты. Делаем проверку:
80+54008,3=54088,3 => верно
Запишем наблюдаемое значение критерия: χ2набл = 54088,3. Выберем уровень значимости ошибки α=0,05. Число степеней свободы равно k = m –2 – 1, где m – число интервалов после объединения. В нашем случае число интервалов после объединения m = 3. Тогда число степеней свободы равно k = 3 – 3 = 0. По таблице критических точек χ2 (Приложение 5) находим χ2кр (0,05; 0) – не существует. Следовательно, есть основания отвергнуть гипотезу о нормальном законе распределения признака Х2 и принять гипотезу Н1.
Зависимость между переменными случайными величинами Х и У, при которой каждому значению одной из них соответствует определенное среднее значение другой величины, называется корреляционной. Функция, описывающая такую зависимость, называется регрессией. По виду функции различают линейную и нелинейную регрессии, по количеству зависимых переменных – одномерную и множественную регрессии. Признак Х, соответствующий независимой переменной, будем называть факторным, признак У, соответствующий зависимой переменной, будем называть результативным. Связь между признаками исследуют с помощью методов наименьших квадратов. Это задача апроксимации функции. Этот метод основан на критерии совпадения функции. Из условия необходимых для существования минимума функции можно получить необходимое число уравнений
для определения неизвестных параметров.

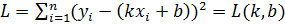
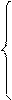   | 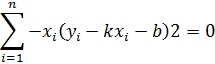  |


Для признаков X1 и Y построим корреляционное поле в системе координат
ХУ, используя исходную таблицу:
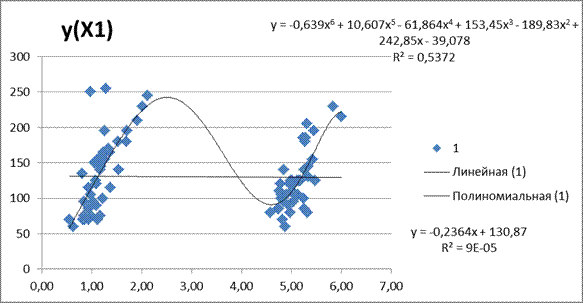
Корреляционное поле на данном рисунке характеризуется набором из 80 точек. Уравнение линейной регрессии имеет вид: у = кх + b, где параметры к и b определяются по методу наименьших квадратов из условия минимального отклонения исходных точек корреляционного поля от прямой регрессии. Для расчета этих величин заполним таблицу:
| # | Y | X1 | X2 | Y*X1 | Y*X2 | x1^2 | x2^2 | x1*x2 |
| 1,09 | 0,031 | 130,8 | 3,72 | 1,19 | 0,000961 | 0,03379 | ||
| 4,99 | 0,042 | 623,75 | 5,25 | 24,90 | 0,001764 | 0,20958 | ||
| 1,69 | 0,046 | 304,2 | 8,28 | 2,86 | 0,002116 | 0,07774 | ||
| 5,15 | 0,033 | 643,75 | 4,125 | 26,52 | 0,001089 | 0,16995 | ||
| 0,93 | 0,03 | 79,05 | 2,55 | 0,86 | 0,0009 | 0,0279 | ||
| 5,04 | 0,024 | 478,8 | 2,28 | 25,40 | 0,000576 | 0,12096 | ||
| 0,86 | 0,07 | 60,2 | 4,9 | 0,74 | 0,0049 | 0,0602 | ||
| 4,97 | 0,03 | 397,6 | 2,4 | 24,70 | 0,0009 | 0,1491 | ||
| 0,99 | 0,03 | 74,25 | 2,25 | 0,98 | 0,0009 | 0,0297 | ||
| 5,05 | 0,051 | 6,12 | 25,50 | 0,002601 | 0,25755 | |||
| 4,87 | 0,014 | 292,2 | 0,84 | 23,72 | 0,000196 | 0,06818 | ||
| 2,11 | 0,03 | 516,95 | 7,35 | 4,45 | 0,0009 | 0,0633 | ||
| 5,48 | 0,04 | 30,03 | 0,0016 | 0,2192 | ||||
| 1,21 | 0,048 | 193,6 | 7,68 | 1,46 | 0,002304 | 0,05808 | ||
| 0,078 | 16,77 | 36,00 | 0,006084 | 0,468 | ||||
| 0,84 | 0,063 | 79,8 | 5,985 | 0,71 | 0,003969 | 0,05292 | ||
| 4,76 | 0,047 | 523,6 | 5,17 | 22,66 | 0,002209 | 0,22372 |
| 1,16 | 0,033 | 2,475 | 1,35 | 0,001089 | 0,03828 | |||
| 5,23 | 0,076 | 967,55 | 14,06 | 27,35 | 0,005776 | 0,39748 | ||
| 1,36 | 0,053 | 224,4 | 8,745 | 1,85 | 0,002809 | 0,07208 | ||
| 1,18 | 0,08 | 171,1 | 11,6 | 1,39 | 0,0064 | 0,0944 | ||
| 5,26 | 0,059 | 447,1 | 5,015 | 27,67 | 0,003481 | 0,31034 | ||
| 0,81 | 0,027 | 109,35 | 3,645 | 0,66 | 0,000729 | 0,02187 | ||
| 5,33 | 0,035 | 692,9 | 4,55 | 28,41 | 0,001225 | 0,18655 | ||
| 2,01 | 0,039 | 462,3 | 8,97 | 4,04 | 0,001521 | 0,07839 | ||
| 5,12 | 0,062 | 7,75 | 26,21 | 0,003844 | 0,31744 | |||
| 1,09 | 0,051 | 98,1 | 4,59 | 1,19 | 0,002601 | 0,05559 | ||
| 5,01 | 0,05 | 626,25 | 6,25 | 25,10 | 0,0025 | 0,2505 | ||
| 1,37 | 0,027 | 157,55 | 3,105 | 1,88 | 0,000729 | 0,03699 | ||
| 4,78 | 0,033 | 573,6 | 3,96 | 22,85 | 0,001089 | 0,15774 | ||
| 4,8 | 0,047 | 4,7 | 23,04 | 0,002209 | 0,2256 | |||
| 4,79 | 0,049 | 502,95 | 5,145 | 22,94 | 0,002401 | 0,23471 | ||
| 5,13 | 0,032 | 538,65 | 3,36 | 26,32 | 0,001024 | 0,16416 | ||
| 1,91 | 0,062 | 401,1 | 13,02 | 3,65 | 0,003844 | 0,11842 | ||
| 5,24 | 0,054 | 5,4 | 27,46 | 0,002916 | 0,28296 | |||
| 1,02 | 0,082 | 96,9 | 7,79 | 1,04 | 0,006724 | 0,08364 | ||
| 4,9 | 0,054 | 514,5 | 5,67 | 24,01 | 0,002916 | 0,2646 | ||
| 1,71 | 0,059 | 333,45 | 11,505 | 2,92 | 0,003481 | 0,10089 | ||
| 5,26 | 0,063 | 736,4 | 8,82 | 27,67 | 0,003969 | 0,33138 | ||
| 0,82 | 0,034 | 57,4 | 2,38 | 0,67 | 0,001156 | 0,02788 | ||
| 4,96 | 0,038 | 595,2 | 4,56 | 24,60 | 0,001444 | 0,18848 | ||
| 1,05 | 0,045 | 157,5 | 6,75 | 1,10 | 0,002025 | 0,04725 | ||
| 5,83 | 0,02 | 1340,9 | 4,6 | 33,99 | 0,0004 | 0,1166 | ||
| 1,54 | 0,032 | 215,6 | 4,48 | 2,37 | 0,001024 | 0,04928 | ||
| 5,27 | 0,059 | 948,6 | 10,62 | 27,77 | 0,003481 | 0,31093 | ||
| 1,12 | 0,066 | 78,4 | 4,62 | 1,25 | 0,004356 | 0,07392 | ||
| 5,34 | 0,023 | 774,3 | 3,335 | 28,52 | 0,000529 | 0,12282 | ||
| 1,17 | 0,039 | 163,8 | 5,46 | 1,37 | 0,001521 | 0,04563 | ||
| 5,42 | 0,052 | 840,1 | 8,06 | 29,38 | 0,002704 | 0,28184 | ||
| 1,52 | 0,089 | 273,6 | 16,02 | 2,31 | 0,007921 | 0,13528 | ||
| 1,23 | 0,029 | 202,95 | 4,785 | 1,51 | 0,000841 | 0,03567 | ||
| 4,95 | 0,022 | 445,5 | 1,98 | 24,50 | 0,000484 | 0,1089 | ||
| 1,28 | 0,062 | 326,4 | 15,81 | 1,64 | 0,003844 | 0,07936 | ||
| 5,32 | 0,063 | 425,6 | 5,04 | 28,30 | 0,003969 | 0,33516 | ||
| 0,55 | 0,047 | 38,5 | 3,29 | 0,30 | 0,002209 | 0,02585 | ||
| 4,85 | 0,026 | 3,64 | 23,52 | 0,000676 | 0,1261 | |||
| 1,08 | 0,047 | 5,875 | 1,17 | 0,002209 | 0,05076 | |||
| 5,01 | 0,037 | 551,1 | 4,07 | 25,10 | 0,001369 | 0,18537 | ||
| 0,94 | 0,025 | 108,1 | 2,875 | 0,88 | 0,000625 | 0,0235 | ||
| 5,28 | 0,029 | 976,8 | 5,365 | 27,88 | 0,000841 | 0,15312 | ||
| 4,85 | 0,023 | 460,75 | 2,185 | 23,52 | 0,000529 | 0,11155 | ||
| 0,63 | 0,025 | 37,8 | 1,5 | 0,40 | 0,000625 | 0,01575 | ||
| 4,82 | 0,038 | 337,4 | 2,66 | 23,23 | 0,001444 | 0,18316 | ||
| 1,22 | 0,036 | 3,6 | 1,49 | 0,001296 | 0,04392 | |||
| 5,05 | 0,035 | 530,25 | 3,675 | 25,50 | 0,001225 | 0,17675 | ||
| 1,26 | 0,042 | 245,7 | 8,19 | 1,59 | 0,001764 | 0,05292 | ||
| 5,18 | 0,052 | 647,5 | 6,5 | 26,83 | 0,002704 | 0,26936 | ||
| 1,06 | 0,053 | 7,95 | 1,12 | 0,002809 | 0,05618 | |||
| 4,73 | 0,038 | 402,05 | 3,23 | 22,37 | 0,001444 | 0,17974 | ||
| 1,33 | 0,059 | 226,1 | 10,03 | 1,77 | 0,003481 | 0,07847 | ||
| 0,85 | 0,037 | 63,75 | 2,775 | 0,72 | 0,001369 | 0,03145 | ||
| 5,45 | 0,052 | 1062,75 | 10,14 | 29,70 | 0,002704 | 0,2834 | ||
| 0,93 | 0,035 | 65,1 | 2,45 | 0,86 | 0,001225 | 0,03255 | ||
| 4,58 | 0,022 | 366,4 | 1,76 | 20,98 | 0,000484 | 0,10076 | ||
| 1,25 | 0,078 | 193,75 | 12,09 | 1,56 | 0,006084 | 0,0975 | ||
| 5,31 | 0,065 | 1088,55 | 13,325 | 28,20 | 0,004225 | 0,34515 | ||
| 1,12 | 0,04 | 173,6 | 6,2 | 1,25 | 0,0016 | 0,0448 | ||
| 4,74 | 0,028 | 402,9 | 2,38 | 22,47 | 0,000784 | 0,13272 | ||
| 0,98 | 0,045 | 102,9 | 4,725 | 0,96 | 0,002025 | 0,0441 | ||
| 0,98 | 0,075 | 18,75 | 0,96 | 0,005625 | 0,0735 | |||
| Суммы: | 251,35 | 3,596 | 32632,3 | 488,525 | 1105,31 | 0,18432 | 10,99131 |
Следовательно параметры регрессии равны:
   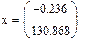 |
k = -0,236, b = 130,868
Окончательно, уравнение линейной регрессии имеет вид: y = -0,236x + 130,868
Определим выборочный коэффициент корреляции по формуле:
r=k (σ x/ σ y)=-0,00964
Проверим коэффициент корреляции на значимость.
Основная гипотеза H0:, rг = 0
Конкурирующая гипотеза H1: rг ≠ 0.
Для проверки гипотезы H0 вычислим наблюдаемое значение критерия:
Tнабл= r(  = -0,08517
= -0,08517
По таблице критических точек распределения Стьюдента найдем критическое значение критерия при уровне значимости ошибки α = 0,05 и числе степеней свободы k = n – 2 = 80 – 2 = 78:
tкр = tкр (0,05; 78) = 1,97. Сравнивая, получим, что ⎪Тнабл ⎪< tкр.
Следовательно, нулевую гипотезу следует принять. Это значит, что коэффициент корреляции не значительно отличается от нуля, и признаки Х1 и У некоррелированы. Найдем коэффициент детерминации, который для случая линейной регрессии равен квадрату коэффициента корреляции: R = r2. Получим: R = (- 0,00964)2=9,298E-05
Для признаков X2 и Y построим корреляционное поле в системе координат ХУ, используя исходную таблицу:

Следовательно параметры регрессии равны:
 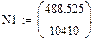  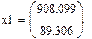 |
k = 908,099, b = 89,306
Окончательно, уравнение линейной регрессии имеет вид y = 908,1x + 89,30
Определим выборочный коэффициент корреляции по формуле:
r=k (σ x/ σ y)=0,314533
Проверим коэффициент корреляции на значимость.
Основная гипотеза H0:, rг = 0
Конкурирующая гипотеза H1: rг ≠ 0.
Для проверки гипотезы H0 вычислим наблюдаемое значение критерия:
Tнабл= r(  = 2,926
= 2,926
По таблице критических точек распределения Стьюдента найдем критическое значение критерия при уровне значимости ошибки α = 0,05 и числе степеней свободы k = n – 2 = 80 – 2 = 78:
tкр = tкр (0,05; 78) = 1,97. Сравнивая, получим, что ⎪Тнабл ⎪> tкр.
Следовательно, нулевую гипотезу следует отвергнуть. Это значит, что коэффициент корреляции значимо отличается от нуля, и признаки Х2 и У коррелированы.
Найдем коэффициент детерминации, который для случая линейной регрессии равен квадрату коэффициента корреляции: R = r2. Получим: R = (0,314533)2=0,0989
Для признаков X2 и Х1 построим корреляционное поле в системе координат ХУ, используя исходную таблицу:

Следовательно параметры регрессии равны:
    |
k = -13,531, b = 3,75
Окончательно, уравнение линейной регрессии имеет вид y = -13,53x + 3,750 Определим выборочный коэффициент корреляции по формуле:
r=k (σ x/ σ y)=-0,1147
Проверим коэффициент корреляции на значимость.
Основная гипотеза H0:, rг = 0
Конкурирующая гипотеза H1: rг ≠ 0.
Для проверки гипотезы H0 вычислим наблюдаемое значение критерия:
Tнабл= r(  = -1,02
= -1,02
По таблице критических точек распределения Стьюдента найдем критическое значение критерия при уровне значимости ошибки α = 0,05 и числе степеней свободы k = n – 2 = 80 – 2 = 78:
tкр = tкр (0,05; 78) = 1,97. Сравнивая, получим, что ⎪Тнабл ⎪< tкр.
Следовательно, нулевую гипотезу следует принять. Это значит, что коэффициент корреляции не значительно отличается от нуля, и признаки Х1 и X2 некоррелированы. Найдем коэффициент детерминации, который для случая линейной регрессии равен квадрату коэффициента корреляции: R = r2. Получим: R = (- 0,1147)2=0,0131
 2015-10-22
2015-10-22 753
753







