Реализация булевых функций F2 подсистемы А на элементах малой интеграции более сложна в связи с необходимостью логического «умножения» выходных сигналов DC (2) в виде τ a i на значения сигналов α 1, α 2, …, αr. Для рассматриваемого примера получим схему рис. 63.
В схемах рис. 62 и рис. 63 у микросхем DC (1) и DC (2) показаны только 10 выходов с номерами 0, 1, …, 9, т.к. остальные выходы DC с 10-го по 15-й не используются в данном примере.
При относительно большом числе логических условий (более 8-12) и числе состояний автомата более 32 увеличение количества элементов «И» и «ИЛИ» для реализации схемы F2 приводит к необходимости применения нескольких десятков микросхем малой и средней интеграции, что ведет к конструктивной сложности печатной платы-сборки и большому числу контактных (паяных) соединений. В этом случае реализация А подсистемы производится на элементах большой интеграции (БИС), т.е. осуществляется реализация комбинационной схемы F2 на ПЗУ или на программируемой логической матрице (ПЛМ).

Рис. 63. Адресная подсистема автомата
При использовании ПЗУ отпадает необходимость в DC (2), т.к. он имеется в составе самого ПЗУ, нет также необходимости формирования унитарного кода f0, f1, …, fi и его преобразования в двоичный код S0, S1, …, S p, т.к. этот код {S} может быть получен сразу на выходе ПЗУ.
Для такой реализации упрощается схема автомата (рис. 64) и меняется правило формирования выходных сигналов {S} как содержимого числового блока ПЗУ, определяемого сводным адресом, т.е. конкатенацией кодов αr,…, α 2, α 1 и Z p,…, Z1, Z0.
В этом случае по графу автомата строится таблица переходов 25, но с явным обозначением кодов {Z} и {S}. Для рассматриваемого примера получим табл. 26.
При использовании ПЗУ нет необходимости выписывать булевы функции F2, т.к. по каждой конкатенации {α}{Z} можно определить выходной код {S}, т.е. определить таким образом содержимое числового блока ПЗУ. Сигнал синхронизации τ будет использоваться как команда считывания ПЗУ. Очевидно, что частота следования импульсов ГИ должна быть согласована с реальным быстродействием работы ПЗУ.
Оценим объем ПЗУ для примера.
Количество переменных {Z} равно 4, мощность множества {α} равна 3, следовательно, число констант – 27. Поскольку разрядность кода {S} равна 4, то объем ПЗУ V = 4∙27 = 29 = 512 бит.
При увеличении числа состояний и логических условий величина V быстро нарастает.

Рис. 64
Пусть мощность множества {Z} равна 6, а q = 12 (q – количество элементов  ), тогда V = 6∙218. Но т.к. ПЗУ разрядностью 6 не выпускаются, то потребуется V = 8∙218 = 221 бит, т.е. объем памяти ПЗУ V > 2 Мб. Такое увеличение объема ПЗУ определяется тем, что в числовом блоке ПЗУ предусмотрены и такие константы, которые не будут соответствовать ни одному реальному сочетанию αr,…, α 2, α 1, т.к. чаще всего на каждом шаге алгоритма проверяется лишь одно, максимум два значения α из { α }*.
), тогда V = 6∙218. Но т.к. ПЗУ разрядностью 6 не выпускаются, то потребуется V = 8∙218 = 221 бит, т.е. объем памяти ПЗУ V > 2 Мб. Такое увеличение объема ПЗУ определяется тем, что в числовом блоке ПЗУ предусмотрены и такие константы, которые не будут соответствовать ни одному реальному сочетанию αr,…, α 2, α 1, т.к. чаще всего на каждом шаге алгоритма проверяется лишь одно, максимум два значения α из { α }*.
Для определения систем булевых функций, подлежащих реализации на ПЛМ, в табл. 25 необходимо внести дополнительно код а(t) и a(t + 1), тогда получим табл. 26, отличающуюся от предыдущей расшифровкой кодов N(t) и N(t + 1).
Таблица 26
| a(t) | N(t) | Услов. Пер. | a(t + 1) | N(t) + 1 |
| Z3, Z2, Z1, Z0 | α3, α2, α1 | S3,S2,S1,S0 | ||
| ~ ~ ~ | ||||
| ~ ~ ~ | ||||
~ ~  ~ ~ α 1
~ ~ α 1
| ||||
~ 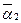 ~
~ α 2 ~ ~
~ α 2 ~
| ||||
| ~ ~ ~ | ||||
| ~ ~ ~ | ||||
 ~ ~ ~ ~
| ||||
| ~ ~ ~ | ||||
| ~ ~ ~ |
По обычному правилу выпишем из полученной таблицы для каждого выхода S i логическую (дизъюнктивную) сумму всех конъюнкций конкатенации { α }{Z}, при которых S i равно «1». Для рассматриваемого примера получим*:



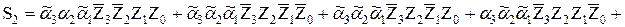

 2015-10-22
2015-10-22 579
579








