Цель: ознакомиться с методами решения экономических задач в условиях конфликтных ситуаций используя математическую модель теории матричных игр на ЭВМ.
Рассмотрим методы принятия управленческих решений в условиях конфликта, когда в ситуации участвуют две стороны, интересы которых противоположны. Это могут быть, например, отношения продавца и покупателя, банка и заемщика, истца и ответчика. Для решения таких задач используют методы теории игр, для анализа которых удобно использовать ЭВМ.
Пусть в игре участвуют два игрока А и В. Игрок А имеет n чистых стратегий, а игрок В – m стратегий. А выигрывает у В сумму a ij, если А выбрал вариант i (i=1,2,…, n), а В выбрал вариант j (j=1,2,…, m). Тогда платежная матрица игры имеет вид:



 a 11 a 12 … a 1m
a 11 a 12 … a 1m
A = [ a ij ] = a 21 a 22 … a 2m
………..
a n1 a n2 … a nm
 | |||
 |
Для нахождения вероятностей pi и qj оптимальных смешанных стратегий необходимо решать прямую и двойственную задачи линейного программирования (ЗЛП) вида:
а) прямая ЗЛП – минимизировать Z = x 1+ x 2+…+ x n
при ограничениях
 a 11 x 1+ a 21 x 2+…+ a n1 x n ≥ 1,
a 11 x 1+ a 21 x 2+…+ a n1 x n ≥ 1,
a 12 x 1+ a 22 x 2+…+ a n2 x n ≥ 1, (5.1)
……………………. ……
a 1m x 1+ a 2m x 2+…+ a nm x n≥ 1,
x 1, x 2,…, x n ≥ 0.
Обращаем внимание: строка ограничения формируется из столбца платежной матрицы!
Решая ее, находим оптимальное решение x 1*, x 2*,…, x n*, откуда, разделив на Z*= x 1*+ x 2*+…+ x n*, получаем оптимальную стратегию для игрока А (р 1*, р 2*,.., рn *), которая заключается в применении i-й чистой стратегии с частотой рi *= хi */ Z*.
б) двойственная ЗЛП – максимизировать F = y 1+ y 2+ … + y m→max;
 при ограничениях
при ограничениях
a 11 y 1+ a 12 y 2+ …+ a 1m y m ≤1;
a 21 y 1+ a 22 y 2+ …+ a 2m y m ≤1; (5.2)
…………………………..
a n1 y 1+ a n2 y 2+ …+ an m y m ≤1;
y 1≥0; y 2≥0; … y m ≥0.
Здесь строка ограничения формируется из строки платежной матрицы.
Решая данную ЗЛП, находим оптимальное решение у 1*, у 2*,…, у m*, откуда, разделив на F *= y 1*+ y 2*+…+ y m*, получаем оптимальную стратегию для игрока B (q 1*, q 2*,.., qm *), которая заключается в применении j-й чистой стратегии с частотой qj *= yj */ F *.
Затем находим цену игры g =1/ Z* =1 /F*.
ПРИМЕР 5.1. Две конкурирующие коммерческие организации А и В выпускают продукцию одного вида. Каждая организация планирует проведение рекламной акции, причем маркетологи каждой компании предложили четыре сценария ее проведения A 1, A 2, A 3, A 4– для компании А и B 1, B 2, B 3, B 4– для компании В. Ожидаемая прибыль для кампании А при каждой ее стратегии Ai и ответе Bj представлена в платежной матрице:
| Ai \ Bj | B 1 | B 2 | B 3 | B 4 |
| A 1 | ||||
| A 2 | ||||
| A 3 | ||||
| A 4 |
Необходимо найти оптимальные стратегии для обоих игроков А и В в предположении, что чем больше выигрыш одного игрока, тем он меньше для другого. Определить среднюю прибыль А.
Рассмотрим задачу со стороны игрока А. Для ее решения нужно составить соответствующую задачу линейного программирования, то есть необходимо найти минимум функции
x 1 + x 2 + x 3 + x 4 →min;
при ограничениях:
70 x 1 + 60 x 2 + 20 x 3 + 50 x 4≥1;
30 x 1 + 50 x 2 + 60 x 3 + 70 x 4 ≥1;
20 x 1 + 40 x 2 + 80 x 3 + 30 x 4 ≥1;
50 x 1 + 80 x 2 + 60 x 3 + 50 x 4 ≥1;
x 1 ≥0; x 2 ≥0; x 3 ≥0; x 4 ≥0.
Для решения данной ЗЛП на ЭВМ также используют надстройку EXCEL «Поиск решения».
Подготовим предварительно в электронной таблице данные.
Запускаем программу MS Excel, вводим в ячейку А1 открывшейся электронной таблицы подпись «Переменные», а в следующие ячейки В1-Е1 произвольные значения переменных x 1, x 2, x 3, x 4. Это вначале могут быть произвольные числа, например единицы. Далее, в ячейку А2 вводим подпись «Целевая», а в соседнюю ячейку В2 значение целевой функции (переключившись в английский режим набора текста): «=B1+С1+D1+Е1» или =SUMM(B1:E1), что означает формулу x 1 + x 2 + x 3 + x 4. В третьей строке вводятся левые части системы ограничений. Для этого переводим курсор в ячейку А3 и вводим в ней текст «Ограничения», а в ячейку В3 формулу «=70*В1+60*C1+20*D1+50*E1», которая соответствует левой части первого ограничения системы. Три остальных ограничения вводим в ячейки С3-В3, а именно,
в ячейку С3: «=30*В1+50*C1+60*D1+70*E1»,
в D3: «=20*В1+40*C1+80*D1+30*E1»,
в ячейку Е3: «=50*В1+80*C1+60*D1+50*E1».
После этого вызываем надстройку Сервис/Поиск решения, в поле «Установить целевую ячейку» даем ссылку на В2. Ниже, в области «Равной», поставить переключатель на минимальное значение. Ставим курсор в поле «Изменяя ячейки», и даем ссылки на переменные, обводя мышью ячейки В1-Е1.
Далее, переводим курсор в поле «Ограничения», и вводим ограничения. Для этого нажимаем на кнопку «Добавить» и в появившемся окне в поле «Ссылка на ячейку» даем ссылку на ячейки, содержащие левые части всех четырех ограничений, которые хранятся в ячейках В3:Е3 (то есть переводим курсор в поле «Ссылка на ячейку» и обводим мышью ячейки В3:Е3). В центральном поле выбираем знак неравенства – ограничения: «≥», в поле «Ограничение» вводим единицу. Нажимаем «ОК». Для ввода дополнительных ограничений x 1≥0; x 2≥0; x 3≥0; x 4≥0 нажимаем «Добавить», в поле «Ссылка на ячейку» ставим курсор и обводим ячейки В1-Е1, выводим в центральное поле «≥», ограничение «0», нажимаем «ОК». Результат на рис.5.1.

Рисунок 5.1 Окно «Поиск решения» прямой ЗЛП
Для запуска вычислений нажимаем кнопку «Выполнить». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и нажимаем «ОК» – видим результат (рис.5.2): x 1=0, x 2 =0,015, x 3 =0,05, x 4 =0, что видно из ячеек В1-Е1.

Рисунок 5.2 Решение прямой ЗЛП примера 5.1
Вводим в А5 подпись «Цена игры», а в соседнюю В5 формулу (переключаясь на английский язык) «=1/(В1+С1+D1+Е1)» или =1/В2. Результат: 50. Это средняя вероятность выигрыша для игрока А. Находим вероятности чистых стратегий в смешанной стратегии р. Для этого вводим в А6 подпись «Р1=», а в соседнюю В6 формулу «=В5*В1», вводим в А7: «Р2=», а в В7 формулу «=В5*С1», в А8: «Р3=», а в В8: «=В5*D1», в А9: «Р4=», в В9: «=В5*Е1». Данные показатели и есть решение задачи (рис.5.3).

Рисунок 5.3 Решение примера 5.1 для игрока А
Рассмотрим теперь решение относительно игрока В.
ЗЛП для игрока В имеет вид:
y 1+ y 2+ y 3+ y 4→ max;
70 y 1+30 y 2+ 20 y 3+ 50 y 4≤1;
60 y 1+ 50 y 2+ 40 y 3+ 80 y 4≤1;
20 y 1+ 60 y 2+ 80 y 3+ 60 y 4≤ 1;
50 y 1+ 70 y 2+ 30 y 3+50 y 4≤1;
y 1≥0; y 2≥0; y 3≥0; y 4≥0.
Переходим на «Лист2» электронной таблицы, щелкнув на соответствующей закладке внизу таблицы. Вводим в ячейки открывшейся чистой электронной таблицы в ячейку А1 надпись «Переменные», а в следующие ячейки В1-Е1 произвольные значения переменных, например, цифры 1. В ячейку А2 вводим подпись «Целевая». Вводим в ячейку В2 значение целевой функции (переключившись в английский режим набора текста): «=B1+С1+D1+Е1», что означает формулу y 1+ y 2+ y 3+ y 4. В третьей строке вводятся левые части системы ограничений. Для этого переводим курсор в ячейку А3 и вводим в ней текст «Ограничения». Переключившись в английский режим клавиатуры, вводим в ячейку В3 формулу «=70*В1+30*C1+20*D1+50*E1», которая соответствует левой части первого ограничения системы.
Вводим в ячейку С3: «=60*В1+50*C1+40*D1+80*E1»,
в D3: «=20*В1+60*C1+80*D1+60*E1»,
в ячейку Е3: «=50*В1+70*C1+30*D1+50*E1».
После этого вызываем в меню «Cервис» надстройку «Поиск решений». В поле «Установить целевую ячейку» даем ссылку на В2. Ниже, в области «Равной», поставить переключатель на максимальное значение.
Ставим курсор в поле «Изменяя ячейки», и даем ссылки на переменные, обводя мышью ячейки В1-Е1. Далее, переводим курсор в поле «Ограничения», и вводим ограничения. Для этого, нажимаем на кнопку «Добавить» и далее в поле «Ссылка на ячейку» обводим ячейки В3:Е3, содержащие левые части всех четырех ограничений, в центральном поле выбираем знак неравенства – ограничения: «≤», в поле «Ограничение» вводим единицу. Нажимаем «ОК». Для ввода дополнительных ограничений y 1≥0; y 2≥0; y 3≥0; y 4≥0 нажимаем «Добавить», в поле «Ссылка на ячейку» ставим курсор и обводим ячейки В1-Е1, выводим в центральное поле «≥», ограничение «0», нажимаем «ОК». Результат на рис.5.4.

Рисунок 5.4 Окно «Поиск решения» обратной ЗЛП
Далее запускаем программу, нажимая «Выполнить». Результат решения обратной ЗЛП в ячейках В1-Е1. Вводим в А5 подпись «Цена игры», а в соседнюю В5 формулу (переключаясь на английский язык) «=1/(В1+С1+D1+Е1)». Находим вероятности чистых стратегий q в смешанной стратегии игрока В. Для этого вводим в А6 подпись «q1=», а в соседнюю В6 формулу «=В5*В1», вводим в А7: «q2=», а в В7 формулу «=В5*С1», в А8: «q3=», а в В8: «=В5*D1», в А9: «q4=», в В9: «=В5*Е1». Данные показатели и есть решение задачи для игрока В (рис.5.5).
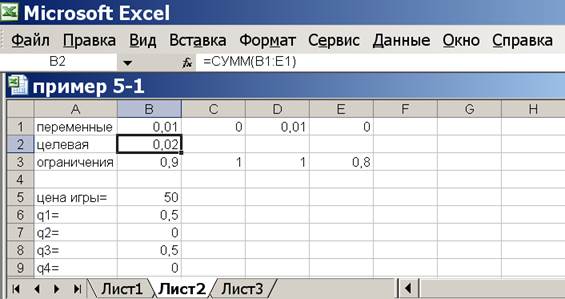
Рисунок 5.5 Решение примера 5.1 для игрока В
ПРИМЕР 5.2. Построить прямую и двойственную задачи линейного программирования для решения матричной игры, заданной платежной матрицей:
A= 
Прямая и двойственная задачи линейного программирования
имеют вид:
x 1 + x 2 + x 3 + x 4 + x 5 →min;
a x 1 + 3 x 2 + 4 x 3 + 6 x 4 + 7 x 5 ≥1;
6 x 1 + a x 2 + 2 x 3 + 3 x 4 + x 5 ≥1;
3 x 1 +5 x 2 + a x 3 +2 x 4 +8 x 5 ≥1;
9 x 1 +2 x 2 +6 x 3 + a x 4 +3 x 5 ≥1;
x i ≥0; i=1,2,3,4,5.
y 1 + y 2 + y 3 + y 4 →max;
a y 1 + 6 y 2 + 3 y 3 + 9 y 4 ≤1;
3 y 1 + a y 2 + 5 y 3 + 2 y 4 ≤1;
4 y 1 + 2 y 2 + a y 3 +6 y 4 ≤1;
6 y 1 + 3 y 2 + 2 y 3 + a y 4 ≤1;
7 y 1 + y 2 + 8 y 3 + 3 y 4 ≤1;
yj ≥0; j=1,2,3,4.
Из решения игры можно найти цену игры
g =1/(x 1 + x 2 + x 3 + x 4 + x 5) =1/(y 1 + y 2 + y 3 + y 4)
и вероятности состояний
pi = xi g, (i = 1,2,3,4,5); qj = yj g, (j =1,2,3,4).
Задание 5.1. Самостоятельно с использованием ЭВМ решить поставленные в примере 5.2 ЗЛП и найти оптимальные смешанные стратегии для игроков А и В.
Значение неизвестного параметра а взять равным номеру варианта.
Отчет должен содержать решения поставленных ЗЛП (значения переменных xi u yj, значения целевых функций), смешанные стратегии для обоих игроков и цену игры g.
Задание 5.2. Директор предприятия А заключает договор с конкурирующей фирмой В о реализации своей продукции на конкретной территории областного центра. Конкурирующие стороны выделили пять районов области. Каждая из них может развивать свое производство в этих пяти районах: A 1, A 2, A 3, A 4, A 5 – для стороны А и B 1, B 2, B 3, B 4, B 5 – для В. Вероятности успеха для стороны А приведены в платежной матрице:
| Ai \ Bj | B 1 | B 2 | B 3 | B 4 | B 5 |
| A 1 | |||||
| A 2 | 30+ а | ||||
| A 3 | 30+ а | ||||
| A 4 | |||||
| A 5 | 30+ а |
Определить оптимальные стратегии для каждой стороны.
Значение неизвестного параметра а взять равным номеру варианта.
Отчет должен содержать математические модели ЗЛП, составленные для игроков А и В, их решения, оптимальные смешанные стратегии для игроков А и В, цену игры g, выводы, в каких районах предприятие А должно реализовывать свою продукцию и в каких пропорциях, чтобы получить оптимальную прибыль вне зависимости от поведения конкурента В и чему равна эта прибыль.
Задание 5.3. Решить игру, описанную платежной матрицей для обоих игроков (матрица приведена для игрока А).
| Аi \ Вj | В 1 | В 2 | В 3 | В 4 | В 5 |
| А 1 | a | ||||
| А 2 | a | ||||
| А 3 | а | ||||
| А 4 | a |
Значение неизвестного параметра а взять равным номеру варианта.
Отчет должен содержать математические модели ЗЛП, составленные для обоих игроков, полученные в результате решения на ЭВМ смешанные стратегии для обоих игроков и цену игры g.
Работа № 6
ИГРЫ С ПРИРОДОЙ
Цель: научиться методам принятия решений в условиях неопределенности и риска (такие математические модели называются Играми с природой) на ЭВМ с использованием критериев Лапласа, Вальда, Байеса, Сэвиджа и Гурвица.
Рассмотрим ситуацию, когда лицо принимающее решение (ЛПР) может выбрать одну из n возможных альтернатив, которые обозначим A 1, A 2,..., A n, то есть выбирает наилучший вариант действий из имеющихся п возможных. Выигрыш для каждой альтернативы зависит от того, какой вариант развития ситуации произойдет. Пусть возможны m вариантов развития ситуации, которые обозначим S 1, S 2,..., S m.
Существует несколько критериев, позволяющих выбрать оптимальное решение в модели игры с природой. Сначала рассмотрим случай, когда показатель привлекательности (выигрыш ЛПР) максимизируется – «чем больше, чем лучше». Рассмотрим на примере способы решения такой задачи.
ПРИМЕР 6.1. Директор финансовой компании проводит рискованную финансовую операцию. Страховая компания предлагает застраховать сделку и предлагает 4 варианта страховки: A 1, A 2, A 3, A 4. Компенсация ущерба для каждого варианта зависит от того, какой из возможных страховых случаев произошел. Выделяют 5 видов страховых случаев: S 1, S 2, S 3, S 4, S 5.Компенсации (тыс. у.е.) для каждого вида страховки при каждом страховом случае составляют матрицу выигрышей вида:
| Ai/Sj | S 1 | S 2 | S 3 | S 4 | S 5 |
| A 1 | |||||
| A 2 | |||||
| A 3 | |||||
| A 4 |
Выбрать наилучшую альтернативу, используя критерии Лапласа, Вальда, Байеса (при вероятностях состояний исходов p 1 = 0,3; p 2 = 0,2; p 3= 0,1; p 4= 0,3; p 5 = 0,1), Сэвиджа и Гурвица (при коэффициенте доверия α=0,4).
Вводим данные в электронную таблицу и готовим подписи в ячейках для дальнейшего расчета согласно рис. 6.1:

Рисунок 6.1 Решение примера 6.1
Вычисляем функции полезности для критерия Лапласа. Для этого ставим курсор в ячейку G2 и вводим формулу, усредняющую значения показателей привлекательности по первой альтернативе. Для этого вызываем мастер функций, нажимая на кнопку fx и выбираем в категории «Статистические» функцию «СРЗНАЧ», в качестве аргумента функции указываем ячейки B2:F2, обводя их курсором. Нажимаем ОК, видим результат 40,2. Автозаполняем ячейки G2-G5, перетаскивая нижний правый уголок ячейки G2. Видно, что наибольшая функция полезности 40,4 для альтернативы А3. Вводим в G6: «А3».
Для критерия Вальда вычисляем наименьшие показатели привлекательности для каждой альтернативы. Для этого вводим в Н2 функцию МИН с аргументами B2:F2: «=МИН(B2:F2)» (кавычки не вводить!). Автозаполняем на Н2-Н5. Выбираем альтернативу, где результат наибольший. Это значение 37 для альтернативы А2, вводим в Н6: «А2».
Для критерия Байеса функции полезности равны суммам выигрышей, умноженным на вероятности их исходов. Вводим в I2 формулу:
«=В2*0,3+C2*0,2+D2*0,1+E2*0,3+F2*0,1», автозаполняем на I2-I5. Выбираем альтернативу с наибольшей функцией полезности, то есть А4, вводим в I6: «А4».
Для критерия Сэвиджа необходимо построить матрицу рисков.
Для этого ставим курсор в ячейку В8 и вводим формулу «=МАКС(B$2:B$5)-B2», автозаполняем результат на ячейки В8-F11.
Далее находим максимальный риск для каждой альтернативы. Для этого ставим курсор в ячейку J2 и вводим «=МАКС(B8:F8)», автозаполняем результат на J2-J5. Выбираем альтернативу с минимальным риском, это А3. Вводим в J6: «А3».
Для критерия Гурвица нужно наибольшее значение каждой альтернативы умножить на α(по условию α= 0,4), наименьшее на (1- α) и результаты сложить. Вводим в К2 формулу:
=МАКС(B2:F2)*0,4+МИН(B2:F2)*0,6 и автозаполняем результат на К2-К5. Выбираем альтернативу с наибольшей функцией полезности. Это А3, вводим К6: «А3». Задача решена.
Рассмотрим теперь метод решения задачи в случае минимизации критерия – «чем меньше, тем лучше».
ПРИМЕР 6.2. Фермер, имея в аренде большие площади под посев кукурузы, заметил, что влажности почвы в сезон созревания кукурузы недостаточно, чтобы получить максимальный урожай. Эксперты советовали фермеру провести дренажные каналы в период конца весны – начала лета, что должно значительно повысить урожай. Были предложены 5 проектов дренажных каналов: A 1, A 2, A 3, A 4, A 5, затраты на которые зависят от погодных условий в период весна – лето.
Возможны варианты: S 1 – дождливая весна и дождливое лето; S 2 – дождливая весна и сухое лето; S 3 – сухая весна и дождливое лето; S 4 – сухая весна и сухое лето. Матрица затрат имеет вид:
| Ai / Sj | S 1 | S 2 | S 3 | S 4 |
| A 1 | ||||
| A 2 | ||||
| A 3 | ||||
| A 4 | ||||
| A 5 |
Выбрать наилучшую альтернативу, используя критерии Лапласа, Вальда, Байеса с p 1 = 0,2; p 2 = 0,3; p 3 = 0,3; p 4 = 0,2, Сэвиджа и Гурвица при коэффициенте доверия α = 0,7.
Вводим данные в электронную таблицу и готовим подписи в ячейках для дальнейшего расчета согласно рис. 6.2:

Рисунок 6.2 Решение примера 6.2
Вычисляем функции полезности для критерия Лапласа. Для этого ставим курсор в ячейку F2 и вводим формулу:
«=СРЗНАЧ(В2:Е2)», автозаполняем на F2-F6. Наилучшей в данном случае считается альтернатива с минимальной функцией полезности, это А2. Вводим в F7: «А2».
Для критерия Вальда вычисляем наибольшие показатели привлекательности для каждой альтернативы. Для этого вводим в G2 функцию «=МАКС(B2:E2)», автозаполняем на G2-G6. Выбираем альтернативу, где результат наименьший, вводим в G7: «А2».
Для критерия Байеса функция полезности вычисляется так же как и для предыдущего примера (но для 4-х состояний природы), в ячейку Н2 формулу «=B2*0,2+C2*0,3+D2*0,3+E2*0,2», автозаполняем на Н2-Н6. Выбираем альтернативу с наименьшей функцией полезности, это А1, вводим в Н7: «А1».
Для критерия Сэвиджа необходимо построить матрицу рисков. Для этого ставим курсор в ячейку В9 и вводим формулу «=B2-МИН(B$2:B$6)», автозаполняем результат на ячейки В9-Е13.
Далее находим максимальный риск для каждой альтернативы. Для этого ставим курсор в ячейку I2 и вводим «=МАКС(B9:E9)», автозаполняем результат на I2-I6. Выбираем альтернативу с минимальным риском, таких альтернатив две, это А1 и А4. Вводим в I7: «А1, А4».
Для критерия Гурвица нужно наименьшее значение каждой альтернативы умножить на α(по условию α= 0,7), наибольшее на (1– α) и результаты сложить. Вводим в J2 формулу:
= МИН(B2:E2)*0,7+МАКС(B2:E2)*0,3
и автозаполняем результат на J2-J6. Выбираем альтернативу с наименьшей функцией полезности. Это А1, вводим J7: «А1». Задача решена.
Задание 6.1. Директор торговой фирмы, продающей телевизоры, решил открыть представительство в областном центре. У него имеются альтернативы либо создавать собственный магазин в отдельном помещении, либо организовывать сотрудничество с местными торговыми центрами. Всего можно выделить 5 альтернатив решения: A 1, A 2, A 3, A 4, A 5. Успех торговой фирмы зависит от того, как сложится ситуация на рынке предоставляемых услуг. Эксперты выделяют 4 возможных варианта развития ситуации S 1, S 2, S 3, S 4.
Прибыль фирмы для каждой альтернативы при каждой ситуации представлена матрицей выигрышей aij (млн. р./год).
| Аi/Bj | S 1 | S 2 | S 3 | S 4 |
| A 1 | a | |||
| A 2 | ||||
| A 3 | a | |||
| A 4 | ||||
| A 5 |
Выбрать наилучшую альтернативу, используя критерии Лапласа, Вальда, Байеса с p 1 = 0,4; p 2 = 0,3; p 3 = 0,1; p 4 = 0,2, Сэвиджа и Гурвица при коэффициенте доверия α = 0,6.
Значение неизвестного параметра а взять равным номеру варианта.
Задание 6.2. Нефтяная компания собирается построить в районе крайнего севера нефтяную вышку. Имеется 4 проекта A, B, C и D.
Затраты на строительство (млн. руб.) зависят от того, какие погодные условия будут в период строительства. Возможны 5 вариантов погоды S 1, S 2, S 3, S 4, S 5. Выбрать оптимальный проект для строительства используя критерии Лапласа, Вальда, Байеса с p 1 = 0,1; p 2= 0,2; p 3= 0,3; p 4= 0,2; p 5 = 0,2, Сэвиджа и Гурвица при α = 0,6. Матрица затрат имеет вид:
| Аi/Sj | S 1 | S 2 | S 3 | S 4 | S 5 |
| A 1 | а | ||||
| A 2 | |||||
| A 3 | a | ||||
| A 4 |
Значение неизвестного параметра а взять равным номеру варианта.
Работа № 7
 2015-10-22
2015-10-22 1233
1233








