В.8 Статистическое оценивание. Точечные оценки параметров распределения

Рассматривая как независимые случайные величины , можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра. Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру θ при любом объеме выборки, т.е. . Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру. Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. Состоятельной называют статистическую оценку, которая при стремиться по вероятности к оцениваемому параметру.

В.9Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Математическое ожидание явл. Функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение M(x)=x_в

В.10 Метод максимального правдоподобия. Пусть есть выборка из распределения , где — неизвестные параметры. Пусть — функция правдоподобия, где . Точечная оценка называется оце́нкой максима́льного правдоподо́бия параметра . Таким образом оценка максимального правдоподобия — это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.Часто вместо функции правдоподобия используют логарифмическую функцию правдоподобия 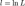. Так как функция монотонно возрастает на всей области определения, максимум любой функции является максимумом функции , и наоборот. Таким образом ,Если функция правдоподобия дифференцируема, то необходимое условие экстремума - равенство нулю ее градиента: Достаточное условие экстремума может быть сформулировано как отрицательная определенность гессиана - матрицы вторых производных: Важное значение для оценки свойств оценок метода максимального правдоподобия играет так называемая информационная матрица, равная по определению 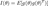В оптимальной точке информационная матрица совпадает с математическим ожиданием гессиана, взятым со знаком минус:

В.11 Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного пара­метра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d, то чем меньше d, тем оценка точнее. число d характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется. Надежностью (доверительной вероятностью) оценки называют вероятность g, с которой осуществляется неравенство |Q—Q* | <d. В.17 Статистическая проверка гипотез. Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений). Этап 1. Располагая выборочными данными и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Но, которую называют основной или нулевой, и гипотезу Н₁ конкурирующую с гипотезой Н₀. Этап 2. Задаются вероятностью a, которую называют уровнем значимости. Этап 3. Находят величину j. Этап 4. Далее рассуждают так. Так как значения критерия позволяют судить о «расхождении выборки с гипотезой Но», то из области допустимых значений критерия j следует выделить подобласть w таких значений, которые свидетельствовали бы о существенном расхождении выборки с гипотезой Но и, следовательно, о невозможности принять гипотезу Но.

В.19 Ошибки первого и второго рода. Ошибка первого рода – отклонение гипотезы H₀ , когда она верна (вероятность ошибки -&-ур. значимости критерия, по которому проверяется справедливость гипотезы H₀). Ошибка второго рода – принятие гипотезы H₀, когда в действительности верна какая-то другая гипотеза (бетта, ее величина зависит от альтернативной гипотезы H₁).