2015-01-21
4713
Понятие интервальной оценки
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому при небольшом объеме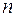 
выборки следует пользоваться так называемыми интервальными оценками.
Статистическая оценка называется интервальной, если она выражается двумя числами – концами интервала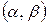 
, покрывающего оцениваемый параметр 
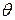. Уточнение понятия интервальной оценки требует введения ряда важных сопровождающих понятий.
Точность оценки. Надежность оценки. Доверительный интервал
Пусть 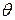– неизвестный оцениваемый параметр теоретического распределения признака Cгенеральной совокупности ( 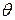есть постоянное число), 
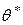– его точечная статистическая оценка, найденная по данным выборки ( 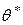– случайная величина, меняющаяся от выборки к выборке). Ясно, что оценка 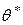тем точнее определяет параметр 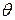, чем меньше модуль разности 
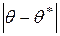. Если рассмотреть неравенство 
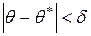, то число 
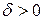будет характеризовать точность оценки (чем меньше 
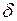, тем оценка точнее).
Итак, точностью оценки 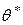называется такое положительное число 
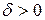, которое удовлетворяет неравенству .
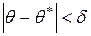Поскольку точечная оценка 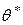является случайной величиной, мы не можем абсолютно доверительно утверждать, что оценка 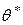будет (при заданной точности 
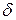) удовлетворять неравенству 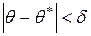. Это неравенство является случайным событием и, следовательно, оно может осуществляться лишь с некоторой вероятностью.
Надежностью (или доверительной вероятностью) оценки 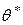называется вероятность 
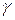, с которой выполняется неравенство 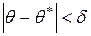, т.е.
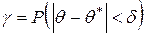(1)
На практике надежность 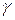назначается (задается наперед): это достаточно большая вероятность (0,95; 0,99; 0,999) – такая, чтобы событие с вероятностью 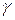можно было считать практически достоверным. Выбор величины 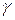диктуется особенностями каждой конкретно рассматриваемой задачи.
Так как неравенство 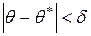равносильно неравенству 
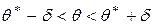, то формулу (1) можно истолковать следующим образом: с заданной надежностью 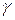интервал 
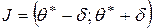накрывает неизвестный оцениваемый параметр 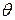. Таким образом, мы приходим к следующему основному определению:
доверительным интервалом для оцениваемого параметра 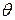называется интервал вида 
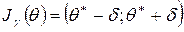, накрывающий неизвестный параметр 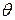с заданной надежностью 
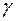(рис.10.).
 |
Границы
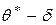и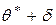 
этого интервала называют доверительными границами. Рис. 10. Доверительный интервал
Найти доверительный интервал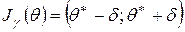 
при заданной надежности 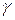– значит найти такое значение точности 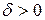, для которого 
.
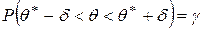2.1.6.3. Доверительный интервал для математического ожидания нормального распределения случайной величины
Пусть в генеральной совокупности нас интересует некоторый признак C, имеющий нормальный закон распределения. Нормальный закон распределения, как мы знаем, содержит 2 параметра: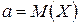 
и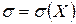 
. Нам требуется найти интервальную оценку для параметра 
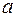этого распределения. (В данном случае неизвестный оцениваемый параметр 
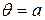.) Для этого необходимо располагать выборочными данными. Пусть по данным некоторой выборки объема 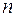вычислена выборочная средняя 
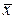– точечная статистическая оценка для математического ожидания 
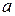(здесь 
).
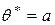Назначим надежность 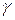. Задача состоит в нахождении доверительного интервала 
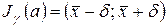, накрывающего математическое ожидание 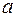с заданной надежностью 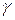. Фактически нужно найти соответствующую точность .
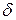Следует различить 2 случая.
В случае "больших" выборок (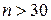
) стандартными в теории вероятностей методами доказывается, что искомая точность 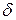вычисляется по формуле
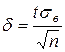, (2)
где величина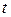 
определяется по специальной таблице значений функции Лапласа, исходя из равенства
.
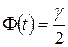Сам же искомый доверительный интервал имеет вид
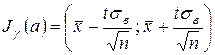
В случае "малых" выборок (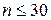
) доказывается, что точность оценивания 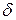находится по формуле:
,
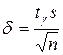где величина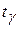 
определяется по специальной таблице Стьюдента значений функции 
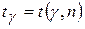[1].
Доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины
В отличие от задачи, представленной в п. 2.1.6.3, здесь роль неизвестного оцениваемого параметра 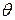выполняет 
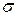, а роль его точечной статистической оценки 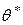– "исправленное" среднее квадратическое отклонение 
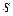, вычисленное по данной выборке объема 
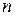. Требуется же найти доверительный интервал 
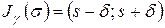при заданной наперед надежности 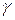. Фактически нужно найти соответствующую точность .
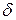Стандартными методами в теории вероятностей устанавливается, что искомая точность оценивания 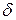вычисляется по формуле
,
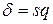где величина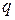 
определяется по специальной таблице значений функции 
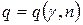[2].
Определение необходимого объема выборки
Назначив (задав наперед) желаемые надежность 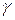и точность 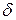, из полученной выше формулы (2) можно рассчитать соответствующий (минимально необходимый) объем выборки:
,
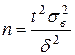при этом величина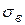 
может быть найдена по результатам пилотажного обследования.
Отметим теперь, что выборка может считаться репрезентативной, если она обеспечивает достижение желаемой точности и надежности получаемых на ее основе статистических оценок.
