Замечательные пределы

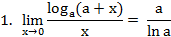
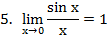
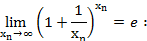
[x_n] ≤ x_n ≤ [x_n]+1

(1 + 1/([x_n]+1))^[xn] < (1 + 1/x_n)^xn ≤ (1 + 1/[x_n])^[xn]+1

(1 + 1/([x_n]+1))^[xn]+1 ⋅ (1/ ( 1+1/([x_n+1]) )) < (1 + 1/x_n)^xn < (1 + 1/[x_n])^[xn] ⋅ (1+1/[x_n])

e e

e

y = -x

(1 – 1/y)^-y = ((y-1)/y)^-y = (y/(y-1))^y = ((y-1+1)/(y-1))^y = (1 + 1/(y-1))^y =

= (1 + 1/(y-1))^y-1⋅(1+1/(y-1)) → e⋅1 = e

z = 1/x

lim_z→0 (1+z)^1/z = e

lim_x→0 (1+x)^1/x = e

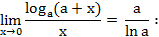
lim_x→0 (ln(1+x))/x = lim_x→0 (1/x)⋅ln(1+x) = lim_x→0 ln(1+x)^1/x = ln (lim_x→0(1+x)^1/x)= ln e = 1

lim_x→0 (log_a(1+x))/x = lim_x→0 (ln (1+x))/(x⋅ln a) = 1/ln a

lim_x→0 (a^x - 1)/x = lim_y→0 y/(loga (1+y)) = ln a

lim_x→0 (e^x - 1)/x = 1

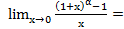lim_x→0 (e^{α⋅ln (1+x)} - 1)/x = lim_x→0 (e^{α⋅ln (1+x)} - 1)/α⋅ln (1+x) ⋅ (α⋅ln (1+x))/x = α

|sin x| ≤ x

x > 0, _B ^C

0 ≤ sinx ≤ x ^{tg x}

0 ≤ (sin x)/x ≤ 1 ^{O A}

S_OAB = S_∆OAC

x/2 ≤ ½ ⋅ 1 ⋅ tg x

x ≤ tg x

x ≤ sinx/cosx,

cosx ≤ sinx/x ≤ 1

1 1 1

Производные

s(t) s(t+h)

s(t), s(t+h), h – приращение.

s’(t) = v(t).

_α

_{a F Q b}

(a,b) f(x)

x₀ ϵ (a,b)

f(x) = x^α, x > 0

x₀ > 0

lim_h→0((x₀ + h)^α – x₀^α)/h = lim_h→0(x₀^α⋅(1 + h/x₀)^α – x₀^α)/h = α ⋅ x₀^{α -1}

∃ f’(x₀), g’(x₀), g(x₀) ≠ 0 ==>

∃ (f/g)’(x₀) = (f’(x₀)⋅g(x₀) – f(x₀)⋅g’(x₀))/(g’(x0))²

lim_h→0 [f(x0+h)/g(x0+h) – f(x0)/g(x0)]⋅1/h =

= lim_h→0(1/h)⋅[(f(x0+h)⋅g(x0) – f(x0)⋅g(x0+h))/g(x0+h)⋅g(x0)] =

= lim_h→0 (1/h)⋅[(f(x0+h)⋅g(x0) – f(x0)⋅g(x0) + f(x0)⋅g(x0) – f(x0)⋅g(x0+h))/g(x0+h)⋅g(x0)] =

= lim_h→0 [(f(x0+h) – f(x0))/h ⋅ g(x0) – (g(x0+h) – g(x0))/h ⋅ f(x0)] ⋅ 1/(g(x0+h)⋅g(x0))

[Σ_k=0ⁿ a_k⋅x^k]’ = Σ_k=1ⁿ a_k⋅kx^k-1

(tg x)’= (sin x/cos x)’ = =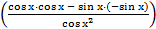

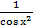
Дифференцирование

f(a) = b

_b

_{a h}

f(a+h) – (α⋅h + β) = ϕ(h) ϕ(h)/h –_h→0→0 = f(a) – β, β = f(a) ==>

f(a+h) – f(a) – α⋅h = ϕ(h) (f(a+h) – f(a) – α⋅h)/h = (f(a+h) – f(a))/h – α –_h→0→ 0 ==>

α = f’(a), т.е. существует «хорошее» линейное приближение <==> существует f’(a) и это линейное приближение имеет вид f’(a)⋅h + f(a) ≈ f(a+h).

Верно и обратное: пусть существует производная, тогда существует такое приближение.

f’(a)⋅h= α⋅h

ϕ(h) = f(a+h) – f’(a)⋅h – f(a) = [f(a+h) – f(a)] – f’(a)⋅h

ϕ(h)/h = (f(a+h) – f(a))/h – f’(a) –_h→0→0

f(x), aϵD,

∃ δ > 0: |x-a| < δ,

x ϵ D ==> f(x) < f(a)

Теорема Ферма

(a,b) f(x)

c ϵ (a,b) – лок. экстремум.

Если в точке с существует производная, то эта производная должна равняться нулю:

∃ f’(c) ==> f’(c) = 0.

Доказательство:

f’(c) = lim_x→c (f(x)-f(c))/(x-c)

Пусть с – локальный максимум, тогда

справа: f(x) ≤ f(c), x>c,

lim_x→c+0 (f(x)-f(c))/(x-c) ≤ 0

слева: f(x) ≤ f(c), x<c, ==> f’(c) = 0.

lim_x→c–0 (f(x)-f(c))/(x-c) ≥ 0

∃ f’(c)

Пусть f(x) определена на [a,b] и

1. f(x) – непрерывна;

2. ∃ f’(x) на (a,b); ==> ∃ ξ ϵ (a,b): f’(ξ) = 0

3. f(a) = f(b);

f(x) непрерывна на (a,b), с ϵ (a,b),

∀ x ≠ c ∃ f’(x)

(a,c) f’(x) ≥ 0 c – точка max

(c,b) f’(x) ≤ 0

∀ x ≠ c ∃ f’(x)

(a,c) f’(x) ≤ 0 c – точка min

(c,b) f’(x) ≥ 0

f’’(x) = (f’)’(x)

f^(n+m)(x) = [f⁽ⁿ⁾]^(m)(x)

[α⋅f(x) + β⋅g(x)]⁽ⁿ⁾ = α⋅f⁽ⁿ⁾(x) + β⋅g⁽ⁿ⁾(x)

Теорема:

Предположим, что f(x), g(x) определена на (a,b), ∃ f⁽ⁿ⁾(x), g⁽ⁿ⁾(x). Тогда

(f⋅g)⁽ⁿ⁾(x) = Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k)(x).

Доказательство:

Докажем по индукции:

(f⋅g)’(x) = f’(x) ⋅ g(x) + f(x) ⋅ g’(x)

(f⋅g)⁽ⁿ⁺¹⁾(x) = d/dx (f⋅g)⁽ⁿ⁾(x) = [(f⋅g)⁽ⁿ⁾]’(x) = [Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k)(x)]’ =

= Σ_k=0ⁿ c_n^k ⋅ [f^(k+1)(x) ⋅ g^(n-k)(x) + f^(k)(x)⋅g^(n-k+1)(x)] =

= Σ_k=0ⁿ c_n^k ⋅ f^(k+1)(x) ⋅ g^(n-k)(x) + Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k+1)(x)

m = k+1:

Σ_k=0ⁿ c_n^k ⋅ f^(k+1)(x) ⋅ g^(n-k)(x) = Σ_m=1ⁿ⁺¹ c_n^m-1 ⋅ f^(m)(x) ⋅ g^(n+1–m)(x)

k = m:

Σ_m=1ⁿ⁺¹ c_n^m-1 ⋅ f^(m)(x) ⋅ g^(n+1–m)(x) + Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k+1)(x) =

= Σ_k=1ⁿ⁺¹ c_n^k-1 ⋅ f^(k)(x) ⋅ g^(n+1–k)(x) + Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k+1)(x) =

= f(x)⋅g(n+1)(x) + f(n+1)(x)⋅g(0)(x) + Σ_k=ⁿ [c_n^k + c_n^k-1]⋅ f^(k)(x) ⋅ g^(n-k+1)(x) =

= Σ_k=0ⁿ c_n^k ⋅ f^(k)(x) ⋅ g^(n-k)(x).

f(x), g(x) g(x) ≠ 0 (x ≠ a)

f(x)/g(x) –_x→a→0 ~ f(x) = o(g(x)) – функция f(x) при x→a стремится к нулю быстрее, чем g(x)

Свойства:

f1(x) = o(g(x))

f2(x) = o(g(x))

1. [f1(x) + f2(x)]/g(x) = f1(x)/g(x) + f2(x)/g(x) → 0

2. f1(x) + f2(x) = o(g(x)) + o(g(x)) = o(g(x))

3. f(x)⋅h(x) = o(g(x)), |h(x)| ≤ M

|f(x)|/|g(x)| ≤ const ~ f(x) = O(g(x)) – порядок малости одинаков у функций f(x) и g(x)

f(x) (a-δ; a+δ), δ>0

∃ f⁽ⁿ⁾(a).

Формула Тейлора

f(x) = Σ_k=0ⁿ (f^(k)(a))/k! (x-a)^k = r_n(x)

r_n(x) = o((x-a)ⁿ), lim_x→a r_n(x)/(x-a)ⁿ = 0

Доказательство:

P_n(x) = Σ_k=0ⁿ (f^(k)(a))/k! ⋅ (x-a)^k

P_n(a) = k!⋅(f^(k)(a))/k! = f^(k)(a)

r_n^(k)(a) = 0, k ≤ n ==> r_n(x) = o((x-a)ⁿ):

n=1. r₁(x) = f(x) – f(a) – f’(a)⋅(x-a) ==> r₁’(a) = 0 => r₁(x) = o(x-a)

r₁(x)/(x-a) = (f(x)–f(a))/(x-a) – f’(a) –_x→a→ 0

n=n-1. r_n’(x) = ϕ(x), ϕ^(k)(x) = r_n^(k+1)(x), x=a => r_n^(k+1)(x) = 0, k+1 ≤ n, k ≤ n-1

ϕ(x)/(x-a)^n-1 –_x→a→ 0

r_n(x)/(x-a)n = (r_n(x) – r_n(a))/(x-a)ⁿ = r_n’(ξ)⋅(x-a)/(x-a)ⁿ = rn’(ξ)/(x-a)^n-1 =

= ϕ(ξ)/(ξ-a)^n-1 ⋅ (ξ-a)^n-1/(x-a)^n-1, ξ ϵ (a,x), ϕ(ξ)/(ξ-a)^n-1 →0, |(ξ-a)^n-1/(x-a)^n-1| < 1 ==>

==> ϕ(ξ)/(ξ-a)^n-1 ⋅ (ξ-a)^n-1/(x-a)^n-1 –_x→a→ 0 ⋅ 1/ℰ = 0.

Разложение по форме Тейлора с остатком в виде Пеано

f’(a) = f’’(a) = … = f^(k-1)(a) = 0

f^(k)(a) ≠ 0, k ≤ n

f(x) = f(a) + 0⋅(x-a) + 0⋅(x-a)² + … + 0⋅(x-a)^k-1 = f^(k)(a)/k! ⋅ (x-a)^k + o((x-a)^k).

f(x) – f(a) = (x-a)^k ⋅[f^(k)(a)/k! + o((x-a)^k)/(x-a)^k]

k – нечётное ==> нет экстремума

sgn = sgn f^(k)(a) k – чётное ==> есть экстремум

f^(k)(a) > 0 ==> f(x) – f(a) ≥ 0 – min

f^(k)(a) < 0 ==> f(x) – f(a) ≤ 0 – max

f(x)/g(x) = [f⁽ⁿ⁾(a)/n! ⋅ (x-a)ⁿ + o((x-a)ⁿ)] / [g^(m)(a)/m! ⋅ (x-a)^m + o((x-a)^m)] =

= [f⁽ⁿ⁾(a)/n! ⋅ (x-a)^n–m + o((x-a)ⁿ)/(x-a)^m] / [g^(m)(a)/m! + o((x-a)^m)/(x-a)^m]

n=m. f(x)/g(x) = [f⁽ⁿ⁾(a)/n! + o((x-a)ⁿ)/(x-a)ⁿ] / [g^(m)(a)/m! + o((x-a)^m)/(x-a)^m]

Вычисление с погрешностью

r_n(x) = (x-a)^p⋅H(x,a,p)

f(x) = Σ_k=0ⁿ (f^(k)(a))/k! (x-a)^k + (x-a)^p⋅H(x,a,p)

ϕ(t) = Σ_k=0ⁿ (f^(k)(t))/k! (x-t)^k + (x-t)^p⋅H(x,a,p), t ϵ (a–δ, a+δ),

∃ ϕ’(t)

ϕ(a) = f(x) t

ϕ(x) = f(x) |––––––––––––|

∃ ξ ϵ (a,x): ϕ’(ξ) = 0 a x

ϕ’(t) = Σ_k=0ⁿ (f^(k+1)(t))/k! (x-t)^k + (-1)⋅k⋅(x-t)^k-1⋅ f^(k)(t))/k! + (-1)⋅p⋅(x-t)^p-1⋅H(x,a,p) =

= f’(t) + f’’(t)⋅(x-t) – f’(t) + f’’’(t)/2! (x-t)² – f’’(t)/2! ⋅2⋅(x-t) + …

… + f⁽ⁿ⁺¹⁾(t)/n! (x-t)ⁿ – f⁽ⁿ⁾(t)/n! ⋅n⋅(x-t)^n-1 – p⋅(x-t)^p-1 ⋅H(x,a,p) =

= f⁽ⁿ⁺¹⁾(t)/n! (x-t)ⁿ – p⋅(x-t)^p-1⋅H(x,a,p)

ξ = a + θ⋅(x–a), 0 < θ < 1

f⁽ⁿ⁺¹⁾(a + θ⋅(x–a))/n! (x–a–θ⋅(x–a))ⁿ = p⋅(x–a–θ⋅(x–a))^p-1⋅H(x,a,p)

f⁽ⁿ⁺¹⁾((x–a)(1–θ))/n! ((x–a)(1–θ))ⁿ = p⋅((x–a)(1–θ))^p-1⋅H(x,a,p)

H = [f⁽ⁿ⁺¹⁾((x–a)(1–θ)) / (n!⋅p)] ⋅ ((x–a)(1–θ))^n+1–p

(x-a)^p⋅H = [f⁽ⁿ⁺¹⁾((x–a)(1–θ)) / (n!⋅p)] ⋅(1–θ)^n+1–p (x-a)ⁿ⁺¹ < погрешности, зависящей от n.

остаток формулы Тейлора в форме Лагранжа: f⁽ⁿ⁺¹⁾(a + θ⋅(x–a))/(n+1)! ⋅(x-a)ⁿ⁺¹

остаток формулы Тейлора в форме Коши: f⁽ⁿ⁺¹⁾(a + θ⋅(x–a))/n! ⋅(1–θ)ⁿ⋅(x-a)ⁿ

= (1+29)^1/3= = 3 = 3⋅(1+1/9)^1/3 = 3⋅[1 + 1/3⋅x – 1/3⋅2/3⋅1/2⋅1⋅x² + 1/3⋅2/3⋅5/3⋅1/(1+θx)^8/3⋅1/3!⋅x³] = 3⋅[ 1 + 1/27 – 1/729 + 5/9⁵⋅1/(1+θx)^8/3];

5⋅3/9⁵ = 5/3 ⋅ 1/9⁴ < 1/3000;

≈ 3 + 1/9 – 1/243 ≈ 3.10699