Границы применимости решения Эйлера. Формула Ясинского

Как показали опыты, решение Эйлера подтверждается не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень работает в пределах упругих деформаций по закону Гука. Следовательно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:

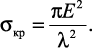(30)

Из (30) следует, что напряжение 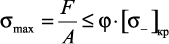возрастает по мере уменьшения гибкости стержня. Заметим, что стержень, имеющий неодинаковые опорные закрепления в главных плоскостях и, следовательно, неодинаковые приведенные длины, теряет устойчивость в той главной плоскости, в которой гибкость стержня имеет наибольшее значение.

Формула Эйлера неприемлема, если напряжения

,

где 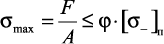– предел пропорциональности. Приравнивая (30) к пределу пропорциональности, получим предельное значение гибкости:

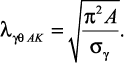
Если λ > λпред, то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст. 3 – l_пред = 100.

В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится нелинейной. В связи с этим, в таких случаях пользуются эмпирическими зависимостями. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:

σ_Еθ = a – bλ, (31)

где a, b – постоянные, зависящие от материала, так для стали Ст. 3 a = 3,1•10⁵ кН/м2, b = 11,4•10² кН/м2.

При гибкостях стержня, находящихся в диапазоне 0 < λ < 40,50, стержень настолько «короток», что его разрушение происходит по схеме сжатия, следовательно, критические напряжения можно приравнять в этом случае к пределу пропорциональности.

Когда формула Эйлера неприменима (за пределом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.

σ_кр = a – bλ, F_кр = σ_крA,

здесь a и b коэффициенты, зависящие от материала стержня, измеряются в МПа, приводятся в справочниках, для ст. 3:

a = 310 МПа, b = 1,14 МПа.

Некоторые термины:

Брус - тело, продольные размеры которого значительно превышают его поперечные размеры.

А) Заделка — нет перемещений (жесткое закрепление тела, например, сварка), возникают реакция неизвестной величины и направления R и реактивный момент MR.

Б) Неподвижная шарнирная опора — возможно вращение вокруг опоры, линейных перемещений нет, поэтому возникает реакция неизвестной величины и направления R, которую заменяют ее проекциями на оси координат. Для плоской системы возникают 2 неизвестные реакции: R1 и R2.

В) Подвижная шарнирная опора — возможно вращение вокруг опоры и перемещение вдоль одной из осей, например, плавающая подшипниковая опора, возникает одна реакция R: сила в направлении ограничения движения

Напряжение (обозначается р).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.

Вектор напряжения можно разложить на две составляющие – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение (обозначается σ) и касательное напряжение (обозначается τ).
Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:

р² = σ² + τ²

Размерности: 1 Мпа = 1 кН / см²

Центр масс —геометрическая точка, характеризующая движение тела или системы частиц как целого.

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.

В основном последние два понятия совпадают, но не всегда. Например (для лучшего осмысления понятия центра тяжести):В системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

Угол поворота - угловое перемещение в радианах.

Если φ — угловое перемещение в радианах, s — длина дуги, заключенной между сторонами угла поворота, r — радиус

φ =s / r = радиан.

Вал – вращающийся стержень.

Дополнение:

Практический метод расчета на устойчивость.

В основу рачетов сжатых стержней на устойчивость положено требование, согласно которому допустимое напряжение должно быть меньше не только предела текучести .

Разделив предел текучести при сжатии на коэффициент запаса по текучести nт получим допустимое напряжение на сжатие для коротких стержней (типа образцов):

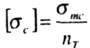Теперь это допустимое напряжение надо еще уменьшить, чтобы оно было меньше . Но критическое напряжение зависит от гибкости стержня (чем больше , тем меньше ) и от материала стойки. Эти факторы учтены в 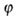-коэффициенте понижения допускаемых напряжений. Коэффициент 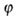берется из таблиц в зависимости от и материала.

Допускаемая сжимающая сила для гибкого стержня определяется по формуле

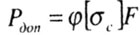где 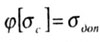- допустимое сжимающее напряжение с учетом устойчивости.

На рис. 8.3 пунктиром дан график зависимости допустимого напряжения ояоп от гибкости стойки .

Различают прямую и обратную задачу проектировочного расчета.

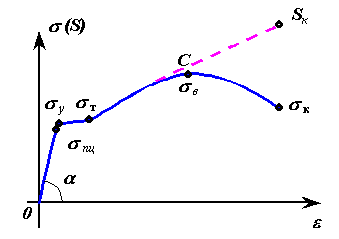
σ _пц - предел пропорциональности – справедлив закон Гука

Определяется как крайняя верхняя точка начального прямолинейного участка диаграммы.

σ _пц = F_пц / A₀

σ _у – предел упругости, это когда выполняется закон Гука, но остаточная деформация приобретает 0.05 % от начальной длины

σ _Т - предел текучести – когда начинается пластическая деформация

Точка после которой линия диаграммы некоторое время движется параллельно оси деформаций ε.

Практически горизонтальный участок диаграммы, следующий за пределом текучести называется площадкой текучести.

σ _Т = F_Т / A₀

σ _пч - предел прочности (σ _в - временное сопротивление) – когда происходит разрыв образца

Высшая точка условной диаграммы;

σ _пч = F_max / A₀

σ _р - напряжение в момент разрыва образца (σ _р^у - условное и σ _р^и - истинное)

Конечная точка диаграммы, при которой происходит разрыв образца.

- условное напряжение разрыва

σ _р^у = F_р / A₀

- истинное напряжение при разрыве

σ _р^и = F_р / A_ш

здесь A_ш - площадь поперечного сечения в области "шейки" образца.

Следует помнить, что предел текучести есть ТОЛЬКО у пластичных материалов!!!

У хрупких материалов условный предел текучести σ_0,2 (читается: сигма ноль-два), который соответствует напряжению, при котором остаточная (пластическая деформация) составляют 0,2 % от длины испытываемого образца.

http://vseshpargalki.narod.ru/Sopromatu.html - очень рекомендую.