Функции. Инъекции, сюръекции, биекции. Понятие последовательности

Отношение называется функцией или отображением из множества А в множество В, если и из (x,y₁) є f, (x,y₂) є f следует y₁=y₂. Если вместо выполняется , то f называется частичной функцией. Функция f из А в В обозначается через или . Если (x,y) є f, то пишем y=f(x) или . Функция называется разнозначной инъективной (инъекцией) или 1-1 функцией если из условия, что выполняется х₁≠х₂, следует y₁≠y₂. Функция называется функцией из А на В или сюръекцией, если . Функция называется взаимно однозначным соответствием между множествами А и В или биекцией, если она инъективна и сюръективна одновременно.

Биекция называется подстановкой.

Утверждения:

1) Если , , то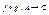

2) Если , то

3) Если f и g - инъекции, то f•g – инъекция.

Доказательство: Предположим противное, т.е. найдутся элементы x₁, x₂, y такие, что х₁≠х₂, (x₁,y) є f•g и (x₂,y) є f•g, т.е. g(f(x₁))=y=g(f(x₂)). В силу разнозначности f имеем f(x₁)≠f(x₂). Отсюда в силу разнозначности g получаем g(f(x₁))≠g(f(x₂)), а это противоречит предположению.

4) Если f,g – сюръекции, то f•g – сюръекция

Доказательство: Нужно доказать, что для любого с существует а такое, что f•g(a)=c. Т.к. g – сюръекция, то существует b, для которого g(b)=c, а т.к. f – сюръекция, то для любого b существует а такое, что f(a)=b. Тогда f•g(a)=g(f(a))=c

5) Если f и g – биекции, то f•g – биекция

6) Если , то