Матрицы бинарных отношений и их свойства. Специальные бинарные отношения

Рассмотрим два конечных множества А={a₁, a₂,…, a_m}, B={b₁, b₂,…, b_n} и бинарное отношение . Определим матрицу [P]=(p_ij) размера бинарного отношения Р по следующему правилу:

Полученная матрица содержит полную информацию о связях между элементами.

Основные свойства матриц бинарных отношений:

1) Если , [P]=(p_ij), [Q]=(q_ij), то и 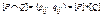, где сложение осуществляется по правилам 0+0=0, 1+1=1+0=0+1=1, а умножение – обычным образом.

2) Если , , то , где умножение матриц [P] и [Q] производится по обычному правилу умножения матриц, но произведение и сумма элементов по определенным в п.1 правилам.

3) Матрица обратного отношения Р^-1 равна транспонированной матрице отношения P: [P^-1]=[P]^T.

4) Если , [P]=(p_ij), [Q]=(q_ij), то p_ij≤q_ij.

5) Матрица тождественного отношения id_A единична: [id_A]=E.

Специальные бинарные отношения:

Пусть Р – бинарное отношение на множестве А:

Отношение Р называется рефлексивным, если для всех выполняется , т.е . Отношение Р называется симметричным, если для любых 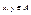из следует , т.е Р^-1=Р, или [P]^T=[P]. Отношение Р называется антисимметричным, если из и следует, что x=y, т.е , или на языке матриц это означает, что в матрице все элементы вне главной диагонали являются нулевыми. Отношение Р называется транзитивным, если из и следует , т.е