Два подхода к определению множества натуральных чисел:
1) Конструктивный.
Позволяет представить натуральные числа в виде объектов, построенных из пустого множества.
Положим по определению 


 . Множества 0, 1, 2,… называются натуральными числами. Объединение этих чисел N={0, 1, 2,…, n,…} называется множеством натуральных чисел.
. Множества 0, 1, 2,… называются натуральными числами. Объединение этих чисел N={0, 1, 2,…, n,…} называется множеством натуральных чисел.
Замечание: АВ – множество всех функций из В в А. Если В=n={0,1,2…,n-1}, A=2={0,1}, то АВ=2n.
2) Аксиоматический подход.
Рассмотрим аксиоматику Дедекинда Пеано:
Пусть имеется некоторое множество N, в котором выбран элемент 0 и функция, которая элементу n из N ставит в соответствие элемент n’ из N, называемый непосредственно следующим (элемент n’ играет роль числа n+1).
Множество N называется множеством натуральных чисел, если система <N,0,’> удовлетворяет аксиомам:
- для любого m≠0 найдется n из N такой, что n’=m.
- для любых m,n из N, если m’=n’, то m=n.
- n’≠0 для любого n из N.
- на множестве N выполняется аксиома математической индукции.
Принцип (аксиома) математической индукции:
Для любого свойства Р (унарного отношения на множестве N), если Р выполняется на элементе 0 (т.е. 0 обладает свойством Р), и для любого n из N из выполнимости Р на элементе n следует выполнимость Р на элементе n’, то свойство Р выполняется на любом элементе n из N.
 или
или  или
или 
Иногда удается установить только выполнение Р(к) для некоторого к>0 и свойство Р(n)=>Р(n+1) для всех n≥к:
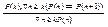
Принцип полной индукции:
Если для всякого n из N из предположения, что P(k) верно при любом натуральном k<n, следует, что P(k) верно также при k=n, то P(n) верно при любом натуральном n:
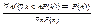
 2015-10-22
2015-10-22 1412
1412
