2015-10-22
1609
Множество – это совокупность объектов, рассматриваемых как единое целое.
Способы задания множеств:
1) Перечисление элементов: М={0,1,2,…,9}
2) Указание свойств Р(х), которым элементы множества должны удовлетворять: М={x | P(x)}.
Неправильное заданные свойства могут привести к противоречию!
Парадокс Рассела:
Рассмотрим множество всех множеств, которые не являются своими собственными элементами: 
. Является ли тогда множество К своим элементом. Если КєК, то должно выполняться свойство, задающее множество К, т.е. К¢К, что приводит к противоречию. Если же К¢К, то, поскольку выполняется свойство, задающее К, то КєК, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
Множество А называется подмножеством множества В, если все элементы А принадлежат В, т.е. 
Множества А и В называются равными или совпадающими, если они состоят из одних и тех же элементов, т.е.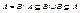 
Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью и обозначается Р(А), т.е. 
. Если |U|=n (множество U содержит n элементов), то |P(U)|=2n.
Множество, не содержащее ни одного элемента называется пустым ø.
Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом U.
1) объединение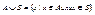 
2) пересечение 
3) вычитание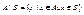 
4) кольцевая сумма (симметрическая разность) 
5) дополнение 
Свойства основных операций над множествами:
1) Ассоциативность: 
2) Коммутативность: 
3) Идемпотентность: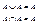 
4) Дистрибутивность: 
5) Поглощение: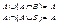 
6) Законы де Моргана: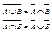 
7) Законы нуля и единицы: 0=ø, 1=U
Упорядоченную последовательность (х1, х2,…,хn) называют кортежем длины n.
Декартовым (прямым) произведением множеств А1, А2,…, Аn называется множество {(x1, x2,…, xn) | x1 є A1,…, xn є An}.
Если А1=А2=…=Аn, то 
– n-ная декартова степень множества А.
А0 = ø
