2015-10-22
2022
Элемент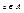 
называется точной верхней гранью (супремумом) множества В (обозначается supB), если а – наименьшая из всех верхних граней множества В. Элемент 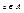называется точной нижней гранью (инфимумом) множества В (обозначается infB), если а – наибольшая из всех нижних граней множества В.
Решеткой называется ЧУМ α=<A,≤>, в котором каждая пара элементов имеет супремум и инфимум. Для заданных элементов 
элемент inf{x,y} называется пересечением элементов x и y (
), а sup{x,y} называется объединением элементов x и y (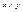
). Заметим, что тогда 
и 
. Наибольший (наименьший) элемент решетки, если он существует, называется нулем (единицей). В конечных решетках всегда есть нуль и единица.
Определим решетку подсистем системы β=<B,∑>, содержащих непустое множество 
. Рассмотрим множество 
и зададим на нем частичный порядок ≤ по следующему правилу: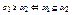 
. Пара <L(β),≤> образует решетку подсистем. В этой решетке для любых систем α1=<A1,∑>, α2=<A2,∑> из L(β) пересечение 
есть подсистема 
, а объединение 
- подсистема, порожденная множеством 
.
Пусть α=<A,∑> - алгебра, Conα={θ | θ – конгруэнция на α}. На множестве конгруэнций Conα зададим отношение ≤ по следующему правилу: θ1≤θ2 <=> для любых элементов 
из условия aθ1b вытекает aθ2b. Это означает, что каждый θ2-класс состоит из θ1-классов. Система <Conα,≤> образует решетку конгруэнций. В этой решетке: для любых тогда и только тогда 
, когда aθ1b и aθ2b; для любых тогда и только тогда 
, когда существуют такие 
, что c1=a, cn=b и справедливо ciθ1ci+1 или ciθ2ci+1 для любого i=1,…, n-1. Решетка конгруэнций имеет нулевую конгруэнцию 
и единичную конгруэнцию 1A=A2.
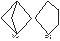Решетка α=<A,≤> называется дистрибутивной, если она подчиняется дистрибутивным законам 
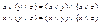для всех 
.
Недистрибутивные решетки:
Критерий дистрибутивности: Решетка α=<A,≤> дистрибутивна тогда и только тогда, когда она не имеет подрешеток, изоморфных М3 или Р5.
