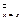Дистрибутивная решетка α=<A,≤> называется булевой алгеброй, если α имеет нуль0, единицу 1, 0≠1 и для любого элемента х из А найдется элемент  (дополнение х) такой, что
(дополнение х) такой, что 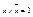 ,
, 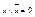 .
.
Утверждение: Если α=<A,≤> - булева алгебра, то для любого элемента х дополнение  единственно.
единственно.
Доказательство: Предположим, что элемент х имеет два дополнения y и z, т.е. 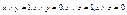 . По закону дистрибутивности получим, что элементы
. По закону дистрибутивности получим, что элементы 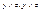 также являются дополнениями х, т.е.
также являются дополнениями х, т.е.  . При этом из y≠z следует, что
. При этом из y≠z следует, что 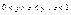 . Отсюда получаем, что подрешетка решетки α с носителем
. Отсюда получаем, что подрешетка решетки α с носителем 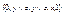 образует решетку Р5, что противоречит дистрибутивности решетки α. Наше допущение неверно.
образует решетку Р5, что противоречит дистрибутивности решетки α. Наше допущение неверно.
Свойства булевой алгебры:
1) Ассоциативность: 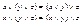
2) Коммутативность: 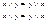
3) Идемпотентность: 
4) Дистрибутивность: 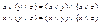
5) Поглощение: 
6) Законы де Моргана: 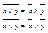
7) Законы нуля и единицы: 0=ø, 1=U
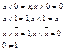
Теорема Стоуна: Любая конечная булева алгебра изоморфна некоторой алгебре Кантора ( )
)
Следствие: Любые две булевы алгебры, имеющие одинаковое число элементов, изоморфны. Число элементов конечной булевой алгебры равно 2n для некоторого 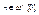 .
.
Таким образом, конечная булева алгебра определяется однозначно с точностью до изоморфизма числом своих элементов.
Принцип двойственности для булевых алгебр: если в справедливом утверждении о булевых алгебрах, касающемся отношения ≤ и операций 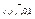 , всюду заменить на
, всюду заменить на  соответственно, то получится также справедливое утверждение, называемое двойственным к исходному.
соответственно, то получится также справедливое утверждение, называемое двойственным к исходному.
Булево кольцо.
Кольцо <R,+,•> называется булевым, если a2=a для всех  .
.
Утверждение: Булево кольцо коммутативно, и a+a=0 для всех элементов  .
.
Доказательство: По определению булева кольца: a+a=(a+a)2=a2+a2+a2+a2=a+a+a+a. Отсюда a+a=0, т.е. a=-a. Также, a+b=(a+b)2=a2+ab+ba+b2=a+b+ab+ba. Отсюда ab+ba=0. Тогда ab=ab+(ba+ba)=(ab+ba)+ba=ba.
Единицей кольца R называется такой элемент e, что a•e=e•a=a, для всех  .
.
Пусть  - булева алгебра. Определим операции кольцевых сложения и умножения на β по следующим правилам:
- булева алгебра. Определим операции кольцевых сложения и умножения на β по следующим правилам: 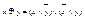 - соответствует кольцевой сумме множеств,
- соответствует кольцевой сумме множеств, 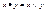 - соответствует пересечению множеств.
- соответствует пересечению множеств.
Теорема: Система 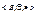 образует булево кольцо с единицей 1.
образует булево кольцо с единицей 1.
Тогда:  ,
, 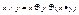 ,
, 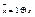 .
.
 2015-10-22
2015-10-22 2147
2147