Многообразия. Теорема Биркгофа

Пусть A_i, - семейство множеств. Декартовым произведением множеств A_i, называется множество

Отметим, что если I={1,2,…,n} – конечное множество индексов, то декартово произведение можно взаимно однозначно рассматривать как множество . Таким образом данное определение согласуется с введенным ранее определением декартова произведения конечного числа множеств.

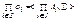Пусть - некоторые алгебры сигнатуры ∑. Декартовым произведением алгебр называется алгебра , в которой функциональные символы 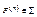интерпретируются по следующему правилу: для любых функций полагаем F(f₁,…, f_n)=f, где f(i)=F_αi(f₁(i),…,f_n(i)) для любого .

Пусть t₁, t₂ - термы сигнатуры ∑. Запись t₁≈t₂ называется тождеством сигнатуры ∑. Она означает, что любые значения, вычисленные по терму t₁, совпадают с соответствующими значениями, вычисленными по терму t₂.

Класс К алгебр сигнатуры ∑ называется многообразием, если существует множество тождеств сигнатуры ∑ такое, что алгебра сигнатуры ∑ принадлежит классу К тогда и только тогда, когда в ней выполняются все тождества из множества Т.

Теорема Биркгофа: Непустой класс алгебр К сигнатуры ∑ тогда и только тогда является многообразием, когда К замкнут относительно подалгебр, фактор-алгебр и декартовых произведений, т.е. класс К вместе с каждой алгеброй содержит любую ее подалгебру, фактор-алгебру, а также вместе с любым семейством алгебр содержит их декартово произведение.