
Множина елементів, кожний з яких входить хоч би в одну з множин сімейства  , називається об'єднанням (сумою) множин.
, називається об'єднанням (сумою) множин.
 .
.
Розглянемо множини  та
та 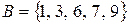 , тоді
, тоді  .
.
 Cукупність елементів множини
Cукупність елементів множини  , які не входять в множину В називається різницею множин
, які не входять в множину В називається різницею множин  і
і  .
.
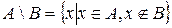 .
.
Якщо розглянути множини, задані в поданому вище прикладі, тоді результатом теоретико-множинної операції різниця буде така множина: 

Множина елементів, кожен з яких входить одночасно у множини  та
та  називається перетином (добутком) цих множин
називається перетином (добутком) цих множин
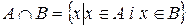 .
.
Перетином двох множин, розглянутих попередньо, буде наступна множина:  .
.

Симетричною різницею множин  і
і 
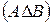 називається множина, яка містить елементи обидвох множин, що не співпадають
називається множина, яка містить елементи обидвох множин, що не співпадають
 .
.
Симетричною різницею розглянутих вище множин  і
і 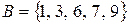 є така множина
є така множина  .
.
 Доповненням множини
Доповненням множини  називається множина, що не містить елементів множини
називається множина, що не містить елементів множини  .
.
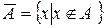
Множина  є доповненням множини
є доповненням множини  до універсальної множини
до універсальної множини  , то
, то  .
.
Якщо за універсальну множину прийняти множину натуральних чисел, то для розглянутої вище множини  , отримаємо
, отримаємо

 2015-10-22
2015-10-22 538
538








