Елементи комбінаторики

Комбінаторний аналіз займається вивченням об’єктів з деякої скінченної множини та їх властивостей. У ролі об’єктів використовуються підмножини множини .

Дамо означення основних комбінаторних об’єктів.

Розміщенням елементів з множини по називається впорядкована підмножина з елементів множини . Впорядкованість означає, що суттєвим є порядок слідування елементів у множині і не допускається повторення елементів. Число всеможливих розміщень з елементів множини по позначається і обчислюється за формулою:

У випадку, коли допускаються повторення одного і того ж елемента у розміщенні, число всеможливих розміщень з повтореннями з елементів множини по обчислюється:

Перестановками називаються всі впорядковані підмножини з n елементів множини .

Очевидно, що перестановки це частковий випадок розміщень при . Число можливих перестановок елементів множини потужності :

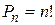
Сполуками (числом комбінацій або вибірками) з елементів множини називають її невпорядковані підмножини (підмножини у класичному розумінні) потужності .

Число можливих сполук з n елементів множини по позначають 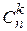або і формула їх обчислення:

Сполуками з повторенням n елементів множини по називаються невпорядковані множини з елементів множини , які можуть повторюватись. Число всеможливих сполук із повтореннями з елементів множини по дорівнює:

Приклади застосування комбінаторики:

1. Обчислення коефіцієнтів бінома Н’ютона:

.

2. Обчислення кількості членів у канонічному представленні многочлена n -го степеня від змінних:

.

3. Визначення коефіцієнтів многочлена степеня від змінних на підставі, так званої, поліноміальної формули:

, де .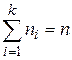

4. Визначення знаку елемента суми при обчисленні визначника матриці n -го порядку:

,

де – деякий добуток елементів матриці, взятих по одному з кожного рядка і кожного стовпця; у випадку, якщо перестановка 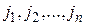парна і , якщо перестановка є непарною.

Наведемо приклади розв'язування задач із застосуванням комбінаторики.

Приклад 1. Скільки існує варіантів вибору 5 телефонних номерів із 10 запропонованих.

Розв’язування. За умовою задачі зрозуміло, що несуттєвим є порядок вибору телефонного номеру, а також неможливо вибрати один і той же номер більше одного разу. Отож, результат даної задачі буде описувати комбінаторний об'єкт, у якому неважливим є місце елемента у комірці, а також неможливі повторення одного елемента в декількох комірках. Тобто це будуть вибірки без повторень із множини 10 елементів у 5 комірок.

.

Приклад 2. Скільки можна утворити телефонних номерів, що складаються із 4 цифр.

Розв’язування. Для утворення телефонного номера використовують цифри {0,1,2,3,4,5,6,7,8,9}. Будемо вважати теоретично можливим телефонний номер із будь-яких 4 цифр. Отже, кожен номер буде містити 4 цифр із 10 можливих. За умовою задачі зрозуміло, що важливим є порядок цифр у номері, а також можливо вибрати одну й ту ж цифру більше одного разу. Отже, результат даної задачі буде описувати комбінаторний об'єкт, у якому важливим є місце елемента у комірці, а також можливі повторення одного елемента в декількох комірках. Тобто це будуть розміщення з повтореннями із множини 10 елементів у 4 комірки.

Зауваження. Оскільки першою цифрою телефонного номера не може бути цифра 0, а лише будь-яка із дев’яти інших, тоді реальна кількість чотирицифрових телефонних номерів визначатиметься так:

Приклад 3. Задано множину .

Встановити, скільки існує вибірок без повторень із елементів цієї множини у 5 комірок за умови, що кожна вибірка повинна містити цифри 7 і 13.

Розв’язування. Оскільки кожна вибірка повинна містити цифри 7 і 13, отже дві комірки із 5 вже зайнято. У три комірки, що залишилися, ми можемо покласти будь-які цифри із множини . Оскільки необхідно визначити кількість вибірок, то неважливим є місце цифр 7 і 13 у комірках, а тому результат будемо знаходити так:

.