Основними об’єктами алгебри логіки є елементарні висловлювання – висловлювання, про які однозначно можна сказати, що вони істинні або хибні.
Кожне елементарне висловлювання алгебри логіки повинно задовольняти двом вимогам:
1) Закон виключення третього. Висловлювання може бути або істинним, або хибним. Третього не дано.
2) Закон протиріччя. Висловлювання не може одночасно бути і істинним, і хибним.
Функцією алгебри логіки (логічною функцією)  від
від  змінних
змінних 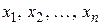 називатимемо функцію, яка приймає значення 0 та 1 (істинне, хибне), і аргументи якої теж можуть приймати значення 0, 1 (істинне, хибне).
називатимемо функцію, яка приймає значення 0 та 1 (істинне, хибне), і аргументи якої теж можуть приймати значення 0, 1 (істинне, хибне).
Серед операцій алгебри логіки визначають наступні:
 – операція заперечення;
– операція заперечення;
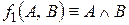 (
( ) – операція кон’юнкції або логічного множення;
) – операція кон’юнкції або логічного множення;
 – операція диз’юнкції або логічного додавання;
– операція диз’юнкції або логічного додавання;
 – операція імплікації;
– операція імплікації;
 – операція еквівалентності або рівнозначності;
– операція еквівалентності або рівнозначності;
 – операція Шеффера;
– операція Шеффера;
 – операція Пірса;
– операція Пірса;
 – операція додавання за модулем два або операція нерівнозначності.
– операція додавання за модулем два або операція нерівнозначності.
Таблиця істинності операцій алгебри логіки.
 |  |  |  |  | 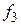 |  |  |  |  |
Пріоритетність логічних операцій (порядок їхнього виконання у формулі при відсутності дужок):
1. операція заперечення;
2. операція кон’юнкції;
3. операція диз’юнкції;
4. усі решта введених операцій зліва направо в порядку входження у формулу.
Розглянемо основні закони операцій алгебри логіки, застосовні до трьох змінних  .
.
1. Закони комутативності 
2. Закони асоціативності 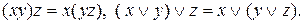
3. Дистрибутивний закон для кон'юнкції по відношенню до диз'юнкції 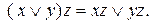
4. Дистрибутивний закон для диз'юнкції по відношенню до кон'юнкції 
5. Закон подвійного заперечення 
6. Закони де-Моргана (закони двоїстості) 
7. Закони ідемпотентності 
8. Закони поглинання 
9. Операції з константами 0 та 1.
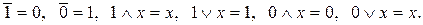
10. Закон виключення третього 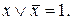
11. Закон суперечливості (протиріччя) 
Справедливість цих законів еквівалентності може бути перевірена за допомогою таблиць істинності.
Алгебраїчна структура  називається алгеброю Буля. Алгебра
називається алгеброю Буля. Алгебра  , побудована на базисі функцій кон’юнкції, додавання за модулем два та функції-константи одиниці, називається алгеброю Жегалкіна.
, побудована на базисі функцій кон’юнкції, додавання за модулем два та функції-константи одиниці, називається алгеброю Жегалкіна.
У алгебрі Жегалкіна виконуються закони:
1. Закони комутативності 
2. Закони асоціативності 
3. Дистрибутивний закон для кон'юнкції по відношенню до додавання по модулю два 
4. Закони ідемпотентності для кон'юнкції 
5. Закон поглинання (зведення подібних членів при додаванні за модулем два 
6. Операції з константами 0 та 1.
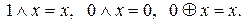
Наведемо еквівалентності, що дозволяють перетворити будь-яку формулу алгебри логіки у формулу алгебри Жегалкіна чи відповідно у формулу алгебри Буля:

Наведемо декілька прикладів розв'язування задач з алгебри логіки.
Приклад 1. Побудувати таблиці істинності формули  .
.
Розв’язування. На підставі таблиці істинності для бінарних логічних операцій побудуємо відповідні таблицю істинності для заданої формули  .
.
Таблиця істинності формули 
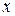 | 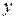 |  |  |  |  |  |  |
Приклад 2. Мінімізувати формулу алгебри логіки, що задана в попередньому завданні.
Розв’язування. Скористаємося побудованою вище таблицею істинності формули  . Побудуємо для кожного її істинного значення відповідну елементарну кон'юнкцію і об'єднаємо їх операцією диз’юнкція (отримаємо відповідну ДДНФ).
. Побудуємо для кожного її істинного значення відповідну елементарну кон'юнкцію і об'єднаємо їх операцією диз’юнкція (отримаємо відповідну ДДНФ).
 =
=  .
.
Далі проведемо неповне склеювання елементарних кон’юнкцій між собою 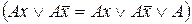 , а також поглинання
, а також поглинання  . Отримаємо скорочену диз’юнктивну нормальну форму, яка визначає кожну формулу однозначно.
. Отримаємо скорочену диз’юнктивну нормальну форму, яка визначає кожну формулу однозначно.
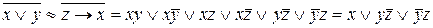 .
.
Подальший аналіз одержаного виразу свідчить про мінімальний рівень складності виразу  , тобто це і є мінімальна ДНФ.
, тобто це і є мінімальна ДНФ.
Приклад 3. Побудувати еквівалентну формулу у алгебрі Жегалкіна для формули, що задана в попередньому завданні.
Розв’язування. Скористаємося наступними співвідношеннями між операціями алгебри логіки:  ;
;  ;
;  , отримаємо
, отримаємо


4. Основні елементи теорії графів.
Предметом перших задач в теорії графів були конфігурації, які можна було зобразити у вигляді точок та ліній, що їх з’єднують. При чому не суттєво, прямі ці лінії чи ні, довгі вони чи короткі, суттєво лише те, що вони з’єднують дві вказані точки.
Граф – це множина точок  , з’єднаних певними способами лініями. Кожна пара вершин
, з’єднаних певними способами лініями. Кожна пара вершин  , що з’єднана лінією, називається ребром графа і позначається
, що з’єднана лінією, називається ребром графа і позначається  . Якщо при розв’язанні задачі суттєвим є напрямок цієї лінії, тоді у графічному зображенні цей напрямок фіксується стрілкою, а ребро називають дугою. Вершини
. Якщо при розв’язанні задачі суттєвим є напрямок цієї лінії, тоді у графічному зображенні цей напрямок фіксується стрілкою, а ребро називають дугою. Вершини  називається початковою, а
називається початковою, а  – кінцевою вершинами дуги
– кінцевою вершинами дуги  . Таким чином, граф G являє собою пару
. Таким чином, граф G являє собою пару  , де
, де  – множина вершин, а
– множина вершин, а  – множина дуг графа.
– множина дуг графа.
Дамо означення деяких основних понять теорії графів.
Дуга  є інцидентною до вершин
є інцидентною до вершин  та
та  , якщо ці вершини є початковою та кінцевою його вершинами.
, якщо ці вершини є початковою та кінцевою його вершинами.
Вершини є інцидентними дузі, якщо дана дуга їх з’єднує.
Дві вершини  та
та  називаються суміжними, якщо вони з’єднані одною дугою.
називаються суміжними, якщо вони з’єднані одною дугою.
Дві дуги 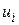 та
та  називаються суміжними, якщо існує спільна для них обох вершина.
називаються суміжними, якщо існує спільна для них обох вершина.
Вершина, не інцидентна жодному ребру, називається ізольованою вершиною.
Вершина, що є початковою вершиною для деяких дуг, але не є кінцевою вершиною жодної дуги, називається вершиною виходу.
Вершина, що є кінцевою вершиною для деяких дуг, але не є початковою вершиною жодної дуги, називається вершиною входу.
Кількість дуг, що виходить з даної вершини називається напівстепенем виходу.
Кількість дуг, що входить у дану вершину називається напівстепенем входу.
Сума напівстепеня входу та напівстепеня виходу називається степенем вершини.
Дуга, початкова та кінцева вершини якої співпадають, називається петлею.
Граф, що складається лише з ізольованих вершин, називається нуль - графом.
Граф, ребрами якого являються всі можливі пари для двох різних його вершин  та
та  , називається повним графом.
, називається повним графом.
Граф називається неорієнтованим, якщо кожне ребро його не орієнтоване, і орієнтованим, якщо орієнтовані всі його ребра. Деколи у графі деякі ребра є орієнтованими, а інші – ні, тоді такий граф називають графом змішаного типу.
Шляхом у графі називають таку послідовність його дуг, у якій кінцева вершина кожної попередньої дуги є одночасно початковою вершиною наступної дуги.
Довжиною шляху називають кількість дуг, що його утворює.
Контуром у графі називають замкнений шлях, тобто шлях, у якому початкова та кінцева вершина співпадають.
Довжиною контура називають кількість дуг, що його утворює.
Шлях називається елементарним, якщо всі вершини, які він містить, є різними.
Контур називається елементарним, якщо всі вершини, які він містить, за винятком початкової та кінцевої, є різними.
Шлях називається простим, якщо всі дуги, які він містить, є різними.
Контур називається простим, якщо всі дуги, які він містить, є різними.
Граф, у якому для будь-якої пари його вершин існує шлях, що їх з'єднує, називається зв’язним.
Зваженим називається граф, у якого кожній його дузі поставлено у відповідність певне невід’ємне число, що називається вагою дуги.
Вагою (довжиною) шляху називається кількість (або сума всіх ваг) дуг, що його утворюють.
Підграфом заданого графа G називається граф, в який входить лише частина вершин графа G з інцидентними дугами.
Частковим графом графу G називається граф, що містить частину дуг основного графа і всі вершини, що належать основному графу G.
Зауваження: для неорієнтованого графа в усіх визначеннях замість поняття дуга використовують поняття ребро, шлях – називають ланцюгом чи маршрутом, а контур – циклом.
 2015-10-22
2015-10-22 1274
1274








