Визначимо поняття еквівалентності та потужності множини на основі взаємно-однозначної відповідності.
Дві множини називають еквівалентними (кількісно еквівалентними), якщо між ними можна встановити взаємно-однозначну відповідність. Іноді стверджують, що це множини з однаковою потужністю  .
.
Множина  , еквівалентна множині натуральних чисел N, називається зчисленною множиною. Властивість зчисленності передбачає, що кожному елементу множини можна поставити у відповідність натуральне число, тобто всі елементи множини можна занумерувати. При цьому:
, еквівалентна множині натуральних чисел N, називається зчисленною множиною. Властивість зчисленності передбачає, що кожному елементу множини можна поставити у відповідність натуральне число, тобто всі елементи множини можна занумерувати. При цьому:
а) будь-яка множина еквівалентна зчисленній множині є зчисленною множиною;
б) будь-які дві зчисленні множини є еквівалентними множинами;
в) будь-яка підмножина зчисленної множини є множиною зчисленною або скінченною;
г) довільне об'єднання скінченної та зчисленної множин є множиною зчисленною.
Поряд із цим, безконечну (нескінченну) множину, яка не є зчисленною, ми будемо називати незчисленною множиною. Множина всіх дійсних точок відрізка (0,1) є множиною потужності континуум. Всі множини, рівнопотужні з нею називатимемо множинами континуальної потужності. Доведено, що множина дійсних чисел є рівнопотужною із множиною всіх дійсних точок відрізка (0,1), а отже, множиною потужності континуум.
Наведемо декілька прикладів розв’язування задач із теорії множин.
Приклад 1. Довести тотожність  .
.
Доведення. Покажемо, що будь-який елемент із множини  є одночасно елементом множини
є одночасно елементом множини  . Для того, щоб
. Для того, щоб  необхідно, щоб
необхідно, щоб  . Аналогічно,
. Аналогічно,  , якщо
, якщо  . З іншого боку, якщо
. З іншого боку, якщо  , то
, то 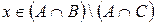 . Отже, якщо
. Отже, якщо  , то
, то  , тобто
, тобто  .
.
Покажемо тепер, що будь-який елемент із множини  буде елементом множини
буде елементом множини  . Нехай
. Нехай  . Якщо
. Якщо  , то
, то  , якщо
, якщо  , то
, то 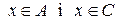 . Отже, якщо
. Отже, якщо 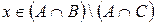 , то
, то  . З іншого боку, якщо
. З іншого боку, якщо  , то
, то  . Аналогічно, якщо
. Аналогічно, якщо  , то
, то  . Отже, якщо
. Отже, якщо 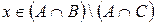 , то
, то  , а значить
, а значить  . Враховуючи попередньо одержане:
. Враховуючи попередньо одержане:  і
і  , матимемо
, матимемо  . Тотожність доведено.
. Тотожність доведено.
Дане завдання можна подати, використовуючи графічну інтерпретацію. Для цього необхідно показати, що область, якій належать елементи множини  співпадає з областю, якій належать елементи множини
співпадає з областю, якій належать елементи множини  , використовуючи діаграми Ейлера-Венна.
, використовуючи діаграми Ейлера-Венна.
Приклад 2. Задано множини  :
:
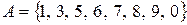 ,
,  ,
,  ,
, 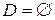 ,
,  . Знайти результат виконання операцій над множинами
. Знайти результат виконання операцій над множинами  .
.
Розв’язування. Виконуючи дане завдання, необхідно використати визначення операцій над множинами, а також деякі з відомих законів.
 ;
;  ;
;  ;
;
Тоді

Отже, обчислимо  .
.
Приклад 3. Задано множини  :
:
 ;
;  ;
;  R – множина дійсних чисел. Чи будуть рівнопотужними множини
R – множина дійсних чисел. Чи будуть рівнопотужними множини  і
і  ?
?
Розв’язування. Очевидно, що обидві задані множини є нескінченними. Визначимо потужність кожної із них. Оскільки множина  містить всі парні числа, кратні 3, вона є підмножиною множини натуральних чисел, а отже, її потужність є зчисленною. Елементами множини
містить всі парні числа, кратні 3, вона є підмножиною множини натуральних чисел, а отже, її потужність є зчисленною. Елементами множини  є всі дійсні числа за винятком натуральних парних чисел. Так як ця множина є підмножиною дійсних чисел, її потужність – континуум. Отже, множини
є всі дійсні числа за винятком натуральних парних чисел. Так як ця множина є підмножиною дійсних чисел, її потужність – континуум. Отже, множини  та
та  не є рівнопотужними.
не є рівнопотужними.
 2015-10-22
2015-10-22 856
856








