МЕТОДИЧНІ ВКАЗІВКИ
До виконання поточних робіт
для студентів базового напрямку 6.0305 – “Філологія”
системи дистанційного навчання
Затверджено
на засіданні кафедри
прикладної математики
Протокол № 6 від 29.12.2006
Львів - 2007
Дискретна математика: Методичні вказівки до виконання поточних робіт для студентів базового напрямку 6.0305 – “Філологія” системи дистанційного навчання / Укл.: О.С.Манзій, І.Є.Тесак. – Львів: Ви-давництво Національного університету “Львівська політехніка”, 2007. - 39 с.
Укладачі Манзій О.С., канд. фіз.-мат. наук, доц.,
Тесак І.Є., ст.викл.
Відповідальний за випуск Костробій П.П., к.ф.-м.н, професор
Рецензенти Гнатів Б.В., канд. фіз.-мат. наук, доц.,
Токарчук М.В., докт. фіз.-мат. наук, проф.
Елементи теорії множин
Під множиною розуміють сукупність елементів, наділених спільними властивостями.
Є два способи задання множин:
а) перелічуванням її елементів;
б) заданням спільної властивості елементів множини.
Перший спосіб застосовний до скінчених множин. Другий – більш універсальний і застосовується для задання як скінчених, так і безконечних множин. Множину прийнято позначати великими літерами (латинськими, грецькими, готичними), наприклад: множина 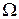 , множина R або
, множина R або 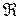 , множина
, множина  . Множину, що не містить жодного елемента, будемо називати порожньою множиною (позначатимемо
. Множину, що не містить жодного елемента, будемо називати порожньою множиною (позначатимемо 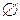 ), тобто порожня множина містить нуль елементів.
), тобто порожня множина містить нуль елементів.
Запис 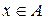 – означає, що елемент
– означає, що елемент 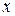 належить множині
належить множині  ;
;
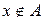 – означає, що елемент
– означає, що елемент 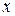 не належить множині
не належить множині  .
.
Приклади задання множин:
а) перечисленням (переліком):
{1, 3, 12} - множина з трьох елементів.
б) заданням властивості:
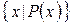 – сукупність всіх елементів
– сукупність всіх елементів 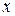 , для яких висловлювання
, для яких висловлювання 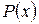 є істинним.
є істинним.
Якщо кожний елемент множини  є разом з тим елементом множини
є разом з тим елементом множини  , то множина
, то множина  називається підмножиною множини
називається підмножиною множини  . Цей факт позначається наступним чином:
. Цей факт позначається наступним чином: 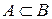 ; якщо ж множина
; якщо ж множина  є підмножиною множини
є підмножиною множини  , цей факт позначають:
, цей факт позначають:  .
.
Поряд із символами включення  та
та 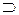 необхідно розрізняти символи
необхідно розрізняти символи  і
і 
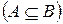 , які означають, що
, які означають, що  включено в
включено в  , і тут не виключений варіант рівності множин. Згідно з цим означенням будь-яка множина
, і тут не виключений варіант рівності множин. Згідно з цим означенням будь-яка множина  є підмножиною самої себе, тобто
є підмножиною самої себе, тобто 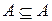 .
.
Порожня множина 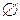 завжди є підмножиною будь-якої множини.
завжди є підмножиною будь-якої множини.
Множину, яка є об’єднанням усіх множин, називають універсальною та позначають літерами  або
або  .
.
Множини та операції над ними можна графічно відобразити за допомогою діаграм Ейлера-Венна.
 2015-10-22
2015-10-22 543
543







