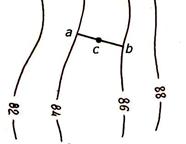
По отметкам точек
Рельефом называют совокупность неровностей земной поверхности. Знание рельефа местности необходимо при проектировании и строительстве железных и автомобильных дорог, осушительных и оросительных систем, промышленных предприятий и т. д. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа штрихами, наносимым на карту по особой шкале.
Рельеф местности может быть также изображен подписями отметок ряда точек или отмывкой красками различного тона. Однако наилучшим способом оказалось изображать рельеф горизонталями в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.
Чтобы правильно изобразить рельеф, необходимо знать его основные формы.
Существует пять основных форм рельефа (рисунок 3.5):
- возвышенность (рисунок 3.5, а);
- котловина (рисунок 3.5, б);
- хребет (рисунок 3.5, в);
- лощина (рисунок 3.5, г);
- седловина (рисунок 3.5, д).
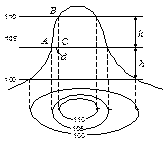
На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности.
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м.
Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
i = h / d = tg υ. (3.6)
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче.
Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
 а) а) |  б) б) |
 в) в) |  г) г) |
 д) д) |
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией).
Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией).
Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом.
Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
Из сущности горизонталей вытекают их свойства:
- горизонталь – это замкнутая кривая линия, все точки на которой имеют одинаковую высоту, кратную высоте сечения рельефа;
- горизонтали на плане не могут раздваиваться и обрываться; если горизонталь не замыкается в пределах плана, она замыкается за его пределом;
- горизонтали не должны пересекаться между собой, так как они получаются пересечением земной поверхности плоскостями, лежащими на разных высотах;
- чем чаще горизонтали на плане, тем уклон местности больше, или чем меньше заложение, тем скат круче;
- водораздельные и водосливные линии и направления максимального уклона горизонтали пересекают под прямым углом.
Высота сечения рельефа устанавливается в зависимости от масштаба плана и характера рельефа местности так, чтобы горизонтали не сливались между собой. В Республике Беларусь приняты следующие высоты сечения рельефа при масштабах съемки:
| 1:500 – h = 0,25; 0,5 м; 1:1000 – h = 0,25; 0,5; 1 м; 1:2000 – h = 0,5; 1; 2 м; | 1:5000 – h = 0,5; 1; 2; 5 м; 1:10000 – h = 1; 2,5; 5 м. |
Для более полного изображения и удобства чтения рельефа на картах и планах подписывают отметки характерных точек рельефа (вершин холмов, дна котловин, перевалов и т. д.). Например, на рисунке 3.5, б подписана отметка дна котловины 98,7 м.
Способы построения горизонталей по отметкам точек.
Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей.
Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется интерполированием горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом.
Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей. 
|
|
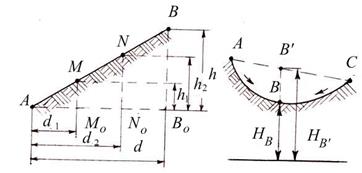
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
d1 = dh1 / h; d2 = dh2 / h,
где h = HB – HA; h1 = HM – HA; h2 = HN – HA.
На плане откладывают отрезки d1 и d2 и получают точки MO и NO, у которых подписывают их отметки. Следует отметить, что интерполирование горизонталей проводят только по линиям с равномерным скатом. На рисунке 3.6, б показан случай неправильной интерполяции между точками А и С с неравномерным скатом местности. Как видно из рисунка, вместо действительного положения точки В будет получена точка В' и соответственно вместо НВ будет получена неверная высота НВ'.
Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пересечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N.
При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
Решение инженерных задач по планам и картам
Современные топографические карты и планы дают богатый и разносторонний материал о той местности, которая на них изображена условными знаками. Зная условные знаки, при изучении карты можно получить необходимые данные о населенных пунктах, гидрографии, растительности, дорожной сети, рельефе и других объектах. Кроме того, при помощи карты можно решать ряд инженерных задач: определять географические и прямоугольные координаты точек, измерять дирекционные углы и азимуты направлений, определять высоты точек, уклоны заданных линий, водосборные площади бассейнов, строить профили земной поверхности, производить трассирование и т. д.
Рассмотрим решение этих задач более подробно.
1. Прямоугольные координаты точек на карте определяют от линии координатной (километровой) сетки, абсциссы и ординаты которых подписываются в общегосударственной системе координат.
2. На картах подписываются также широты и долготы точек пересечения параллелей и меридианов, ограничивающих данный лист. Кроме того, на обрамляющих карту рамках вычерчиваются одноминутные деления широты и долготы. Соединяя точки одноименных делений северной и южной сторон рамок, а также западной и восточной, получим на карте сетку меридианов и параллелей, пользуясь которой, можно определить широту и долготу любой точки карты.
3. Дирекционный угол или азимут линии можно измерить транспортиром непосредственно на карте, как угол между направлением линии километровой сетки или истинного меридиана и направлением заданной линии. Обычно на полях карты всегда дается для данного листа сближение меридианов и склонение магнитной стрелки, используя которые, по формулам (2.3) – (2.4) можно вычислить все углы ориентирования.
4. Высоту (отметку) любой точки, например С (рисунок 3.8, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.
Из подобия треугольников abb1 и acc1, учитывая, что h – высота сечения рельефа, d – заложение (рисунок 3.8, б), получим cc1 = ac bb1 / ab или Δh = Δd h /d. (3.7)
Отметка точки НС будет равна отметки точки a плюс величина Δh:
НС = Нa + Δh.
а) |  б) б) |
Рисунок 3.8 – Определение отметки точки
В формуле (3.7) величины d и Δd измеряют на плане, а высота сечения рельефа известна на плане или карте.
5. Определяют уклон линии. Уклоном линии называется тангенс угла наклона этой линии или отношение высоты сечения рельефа к заложению (рисунок 3.8, б):
i = tg υ = h / d. (3.8)
Для определения уклона можно воспользоваться формулой (3.6) или (3.8). Из формул следует, что уклон – безразмерная величина. Его выражают в процентах (% – сотых долях) или в промилях (‰ – тысячных долях). Для определения угла наклона линии (крутизны ската) υ из формулы (3.8) можно получить:
υ = arctg i = arctg (h / d). (3.9)

Угол наклона можно также определить графически с помощью графика заложений, который обычно приведен под южной рамкой карты. При отсутствии графика заложений его можно построить. Для этого на горизонтальной прямой АВ от точки А откладывают равные отрезки произвольной величины (рисунок 3.9). Из точек отложения к прямой АВ восстанавливают перпендикуляры. Используя формулу (3.8), определяют заложение:
d = h / tg υ = h / i, (3.10)
где h – высота сечения рельефа
Подставляя в формулу (3.10) величины υ, равные 1, 2, 3о и т. д., последовательно получают заложение для каждого из углов наклона υ и откладывают их на перпендикулярах в масштабе плана или карты. Полученные на перпендикулярах точки соединяют плавной кривой линией, а внизу подписывают углы наклона.
Для определения угла наклона по графику заложений с помощью циркуля-измерителя измеряют величину заложения на плане (ab) и прикладывают раствор измерителя к графику заложений так, чтобы одна игла измерителя находилась на основании графика, а вторая располагалась параллельно вертикальным линиям графика, и перемещают измеритель по горизонтальной линии основания вправо или влево до совпадения верхней иглы с кривой графика. По росписи графика заложений отсчитывают крутизну ската. Например, на рисунке 3.9 при заложении ab крутизна ската υ = 1,4о. По графику заложений можно решать и обратную задачу, т. е. по заданной крутизне ската определять величину заложения на плане.
6. Для построения по заданному направлению АВ на плане профиля линии местности при помощи полоски бумаги линия с плана переносится на миллиметровую бумагу с отметками всех точек пересечения линии с горизонталями. Далее в заданном вертикальном масштабе по вертикальным линиям откладывают отметки точек, и все вершины перпендикуляров соединяют прямыми линиями. Получают профиль местности по заданному направлению (рисунок 3.10).
7. Для проведения на карте или плане линии заданного уклона по графику заложений или, исходя из формулы (3.10), определяют величину заложения соответствующего уклона. Затем циркулем-измерителем откладывают это заложение в масштабе плана и, начиная от первой горизонтали, пересекающей линию, последовательно засекают смежные горизонтали. Полученная ломаная линия будет иметь заданный уклон (рисунок 3.11).
 |
Рисунок 3.10 – Продольный профиль
8. Водосборные площади по картам и планам определяют для вычисления расхода воды с бассейнов при строительстве плотин, мостов, труб и т. п. Водосборной площадью или бассейном водотока называют ту площадь, с которой поверхностные воды после дождя или таяния снега по условиям рельефа местности и его геологического строения стекают в данный водоток. Границами водосборной площади служат водораздельные линии и линии наибольшего ската. На карте или плане сначала намечают границы водосборной площади до створа строящегося сооружения, а затем при помощи планиметра или палетки определяют площадь в пределах установленной границы (рисунок 3.12).
|  | |||
| Рисунок 3.11 – Линия заданного клона | Рисунок 3.12 – Определение границы водосборной площади |
Решение практических задач на планах и картах подробно изложено в учебно-методических пособиях по выполнению расчетно-графических и лабораторных работ по геодезии.
Определение площадей по картам и планам
При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам.
Существует три основных способа определения площадей:
- графический, когда площадь вычисляется по данным, взятым графически с плана или карты;
- аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям – координатам вершин участка;
- механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.
Часто эти способы применяются комбинированно. Например, общая площадь участка определяется аналитическим способом, а площадь внутренних контуров – графическим или механическим. Рассмотрим каждый из вышеуказанных способов более подробно.

Графический способ определения площадей. Сущность этого способа состоит в том, что данный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже – прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры.
Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка. Ошибка определения площади графическим способом равна примерно 1:100 – 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.
Площади криволинейных контуров удобно определять при помощи палеток. Палетка (рисунок 3.13) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Пользование палеткой видно из рисунка 3.13. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура.
Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Точность определения площадей палеткой несколько ниже, описанного выше графического способа. Главная ошибка при этом происходит от оценки частей неполных квадратов на глаз. Более высокую точность дают палетки с меньшей стороной квадрата.
Аналитический способ определения площадей. Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.
Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 3.14), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 3.14 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:
Р = 0,5 [(Х1 + Х2) (Y2 – Y1) + (X2 + X3) (Y3 – Y2) –
– (X3 + X4) (Y3 – Y4) – (X4 + X1) (Y4 – Y1)]. (3.11)
Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:
2Р = Х1(Y2 – Y4) + X2(Y3 – Y1) + X3(Y4 – Y2) + X4(Y1 – Y3)
или в общем виде для n-угольника можно записать
n
2Р = ΣХi (Yi+1 – Yi-1). (3.12)
i = 1
Подобным образом из уравнения (3.11) после преобразований можно получить:
2Р = Y1(X4 – X2) + Y3(X1 – X3) + Y3(X2 – X4) + Y4(X3 – X1)
 или n
или n
2Р = ΣYi (Хi-1 – Xi+1). (3.13)
i = 1
Согласно формулам (3.12) и (3.13) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.
Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (3.12) и (3.13). Погрешность вычисления площадей аналитическим способом не превышает 1:1000 вычисляемой площади.
Механический способ определения площадей. Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 3.15), состоящий из полюсного и обводного рычагов.
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3.15), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.
Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.

Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3.15 составит 3215.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
Р = С(U2 – U1), (3.14)
а при полюсе внутри фигуры –
Р = С(U2 – U1 + g), (3.15)
где С – цена деления планиметра;
g – постоянное число планиметра.
Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число.
При проверке планиметра должны быть проверено выполнение следующих условий:
- счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний. Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.
- плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага. Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.
Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры.
Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:
С = Р/ (U2 – U1)ср. (3.16)
После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры.
Постоянное число планиметра:
g = P/C – (U2 – U1). (3.17)
При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.
При определении площадей планиметром необходимо соблюдать следующие правила:
- план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
- положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
- обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
- для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см2) ошибка определения площади планиметром не превышает 1:200 величины площади.
 2015-10-22
2015-10-22 53489
53489