Средняя квадратическая погрешность функции

Измерения величин

В геодезии часто нужно определить точность не только самих измеренных величин, но и их функций. Например, горизонтальное проложение линии является функцией наклонности расстояния и угла наклона, площадь определяемая планиметром является функцией отсчетов по планиметру и т. д. Поэтому важно уметь вычислять средние квадратические погрешности функций. Рассмотрим некоторые виды функций.

1 Функция суммы двух аргументов

φ = Х + Y, (4.19)

где Х и Y – независимо измеренные величины.

Допустим, что каждая из этих величин измерялась n раз и каждое из измерений сопровождалось случайными погрешностями Δ_Х и Δ_Y. Тогда и функция φ, вычисленная по формуле (4.19), будет иметь погрешность Δ_φ:

φ + Δ_φ = (X + Δ_X) + (Y + Δ_Y) или Δ_φ = Δ_Х + Δ_Y. (4.20)

Возведем равенство (4.20) в квадрат:

Δ = Δ + Δ + 2Δ_X Δ_Y. (4.21)

Таких равенств может быть получено n. Сложив их и разделив на n, получим

[Δ ] / n = [Δ 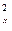] / n + [Δ 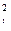] / n + 2[Δ_XΔ_Y] / n. (4.22)

На основании четвертого свойства случайных погрешностей величина [Δ_X Δ_Y] как сумма случайных погрешностей будет стремиться к нулю. Тогда с учетом равенства (4.5) будем иметь:

m 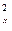= m + m 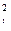. (4.23)

Нетрудно убедиться, что формула (4.23) будет верна и для функции

φ = X –Y. (4.24)

Аналогично предыдущему можно доказать, что для функции суммы (разности) нескольких аргументов

φ = ±Х ± Y ± Z ± … ± U. (4.25)

Квадрат средней квадратической погрешности этой функции будет равен сумме квадратов средних квадратических погрешностей аргументов:

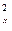m 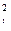= m + m + m +…+ m . (4.26)

Если m_X = m_Y = m_Z = …=m_U, а число измеренных величин X, Y, Z, …, U равно n, то

m 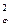= nm² или m_φ = m√ n, (4.27)

т. е. средняя квадратическая погрешность суммы равноточно измеренных величин в √n раз больше средней квадратической погрешности отдельного измерения.

П р и м е р. Найти среднюю квадратическую погрешность суммы измеренных углов в четырехугольнике, если средняя квадратическая погрешность одного угла равна ±30^''. По формуле (4.27) находим

__

m_φ = ± 30^'' √ 4 = ±60^'' = 1^'.

2 Функция линейного вида

φ = КХ,

где К – постоянное число;

Х – аргумент, полученный из измерений.

Если Х будет измерен со случайной погрешностью Δ_Х, то функция будет иметь случайную погрешность

Δ_φ = К Δ_X. (4.29)

Измерив аргумент n раз, можно составить n уравнений (4.29), взять сумму их квадратов и разделить на n. После чего получим

[Δ ] / n = K² [Δ ] / n или m 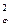= K² m , (4.30)

откуда

m_φ = K m_X. (4.31)

Аналогично предыдущему можно показать, что для функции

φ = ± K₁X ± K₂Y ± … ± K_nU (4.32)

получим

Δ_φ = K₁Δ_X ± K₂Δ_Y ± … ± K_nΔ_U (4.33)

или

m 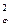= (K₁m_X)² + (K₂m_Y)² + … + (K_nm_U)². (4.34)

П р и м е р. Определить среднюю квадратическую погрешность M арифметической середины L, если средняя квадратическая погрешность отдельного измерения равна m. Напишем формулу (4.4) арифметической середины в следующем виде:

L = l₁ / n + l₂ / n + … + l_n / n. (4.35)

Как видно, здесь можно применить формулу (4.34) для функции (4.35):

m = M ² = (m₁ / n)² + (m₂ / n)² + … + (m_n / n)².

Учитывая, что измерения l₁, l₂,…, l_n равноточные, т. е. m₁ = m₂ = … = m_n, получим

M ² = n(m / n)² = m² / n,

или __

M = m / √n, (4.36)

т. е. средняя квадратическая погрешность арифметической средины в √n раз меньше средней квадратической погрешности отдельного измерения.

3 Функция общего вида

φ = f (X, Y, Z, …,U), (4.37)

где X, Y, Z, …,U – независимо измеренные величины.

С учетом случайных погрешностей функция (4.37) примет вид

φ + Δ_φ = f (X + Δ_X; Y + Δ_Y; Z + Δ_Z; …; U + Δ_U). (4.38)

Разложив функцию (4.38) в ряд Тейлора и ограничившись только первыми степенями случайных погрешностей, получим функцию

Δ_φ = (∂f/∂x) Δ_X + (∂f/∂y) Δ_Y + (∂f/∂z) Δ_Z + … + (∂f/∂u) Δ_U, (4.39)

где (∂f/∂x), (∂f/∂y), …, (∂f/∂u) – частные производные, которые для функции

(4.39) являются постоянными величинами.

Как видно, функция (4.39) аналогична функции (4.33). Следовательно, квадрат ее средней квадратической погрешности

= (∂f/∂x ∙ m_X)² + (∂f/∂y ∙ m_Y)² + (∂f/∂z ∙ m_Z)² + … + (∂f/∂u ∙ m_U)². (4.40)

П р и м е р. В прямоугольнике измерены две стороны – Х = 200 м и Y = 100 м со средними квадратическими погрешностями m_X = +0,20 м и m_Y = +0,10 м.

Определить площадь прямоугольника Р и ее среднюю квадратическую погрешность m_P.

P = XY; ∂p/∂x = Y; ∂p/∂y = X;

= (∂p/∂x)² + (∂p/∂y)² = Y ² + X² =

____ = 100² ∙ 0,20² + 200² ∙ 0,10² = 800 м²;

M_p = √ 800 ≈ ±28 м²; Р = 200 × 100 = 20000 м² ± 28 м².