Неравноточные измерения

В предыдущих разделах были рассмотрены равноточные измерения. Однако на практике часто производятся и неравноточные измерения, которые выполнены в различных условиях или приборами различной точности, различным числом приемов. В этом случае уже нельзя ограничиваться простым арифметическим средним, здесь надо учитывать степень надежности каждого результата измерений.

Степень надежности результата измерения, выраженная числом, называется весом этого измерения. Чем надежнее результат, тем больше его вес. Пусть имеем ряд средних значений: L₁, L₂, …, L_n – одной величины, полученных из Р₁, Р₂, …, Р_n отдельных измерений.

Согласно формуле (4.4) произведение L_i P_i будет равно сумме отдельных измерений l_i в данном ряду, а сумма всех измерений во всех рядах будет равна L₁P₁ + L₂P₂ + … + L_n P_n. Число всех измерений будет равно P₁ + P₂ +…+ P_n.

Отсюда по правилу арифметической средины получим среднее значение из всех рядов измерений:

L_o = (L₁P₁ + L₂P₂ + … + L_nP_n) / (P₁ + P₂ + … +P_n) = [LP] / [P]. (4.44)

Выражение (4.44) называется формулой весового среднего или общей арифметической середины. Здесь число измерений Р₁, Р_2,…, Р_n в каждом ряду является весом средних результатов L₁, L₂, …, L_n, а сумма весов является весом общей арифметической средины L_o. Во всех случаях, когда известны результаты измерений и их веса, вероятнейшее значение измеренной величины вычисляют по формуле (4.44).

Обозначим среднюю квадратическую погрешность одного измерения через μ, а средние квадратические погрешности величин L₁,L₂….L_n соответственно через m₁, m₂, …, m_n. Тогда, согласно равенству (4.36), можем написать, что ___ __ __

m₁ = μ / √ P₁; m₂ = μ / √ P₂; …; m_n = μ / √ P_n. (4.45)

Если в формуле (4.45) принять P_i = 1, то μ = m_i. Отсюда следует, что μ является средней квадратической погрешностью измерения, вес которого равен единице или так называемой средней квадратической погрешности единицы веса.

Из формул (4.45) получим:

__ __ __

μ = m₁ √ P₁ = m₂ √ P₂ = … = m_n √ P_n,. (4.46)

Из равенства (4.46) можно сделать вывод, что произведение всякой величины на корень квадратный из ее веса будет иметь вес, равный единице, что позволяет приводить неравноточные измерения к равноточным.

Из формулы (4.45) можно получить также общее математическое выражение веса:

P_i = μ² / m 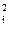, (4.47)

т. е. вес измерения обратно пропорционален квадрату его средней квадратической погрешности. В частном случае, когда μ² = 1,

P_i = 1 / m 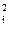. (4.48)

Для вывода средней квадратической погрешности единицы веса обозначим истинные случайные погрешности величин L₁, L₂, …, L_n через Δ₁, Δ₂, …, Δ_n. Тогда для ряда

__ __ __

L₁√ P₁; L₂√ P₂; …; L_n√ P_n

истинные погрешности будут

__ __ ___

Δ₁√ P₁; Δ₂√ P₂; …; Δ_n√ P_n. (4.49)

Ряд (4.49) равноточный, так как согласно формулам (4.31) и (4.46) средние квадратические погрешности его составляющих

__

m_i√ Pi = μ.

Для равноточных измерений погрешность μ можно получить по формуле Гаусса (4.5): ________

μ = √ [PΔ²] / n. (4.50)

По аналогии с формулой (4.50) можем написать выражение средней квадратической погрешности единицы веса через вероятнейшие погрешности V_i величины L_i (уклонения величины L_i от весового среднего L_o):

____________

μ = √ [PV²] / (n – 1). (4.51)

Как видно, формулы (4.50) и (4.51) являются соответственно формулами Гаусса и Бесселя для неравноточных измерений.

Для вывода средней квадратической погрешности М_о общей арифметической середины L_o с весом [Р] и средней квадратической погрешности единицы веса μ воспользуемся соотношением (4.46):

___

μ = М_о√ [Р],

откуда ___

М_о = μ / √ [Р]. (4.52)

П р и м е р. Получены два результата измерения одной и той же линии и известны их средние квадратические погрешности:

L₁ = 175,46 м; m₁ = ± 0,10 м; L₂ = 175,24 м; m₂ = ± 0,20 м;

Определить вероятнейшее значение длины линии и его среднюю квадратическую погрешность.

По формуле (4.48), принимая μ = 1, определим веса результатов измерений:

Р₁ = 1/m²₁ = 1/(0,10)² = 100; Р₂ = 1/m²₂ = 1/(0,20)² = 25.

Затем по формуле (4.44) и (4.52) находим вероятнейшее значение длины линии и его среднюю квадратическую погрешность:

L_o = (L₁P₁ + L₂P₂) / (P₁ + P₂) = (175,46 ∙ 100 + 175,24∙25) / (100 + 25) = 175,42 м;

__ ___

М_о = μ / √[Р] = 1/√125 ≈ 0,09 м.

Тогда вероятнейшее значение длины линии будет

L_o = 175,42 м ± 0,09 м;