Пусть из генеральной совокупности извлечена выборка, причем х 1 наблюдалось п 1 раз, х 2 – п 2 раз, хк – пк раз и 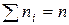 - объем выборки. Наблюдаемые значения х 1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.
- объем выборки. Наблюдаемые значения х 1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.
Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой 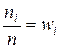 .
.
Определение. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант 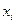 и соответствующих им частот пi или относительных частот
и соответствующих им частот пi или относительных частот 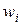 .
.
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
| х1 | х2 | … | 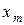 |
| п1 | п2 | … | 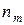 |
(сумма всех частот равна объему выборки 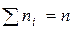 )
)
или в виде таблицы распределения относительных частот:
| х1 | х2 | … | 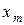 |
| w1 | w2 | … | 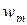 |
(сумма всех относительных частот равна единице 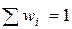 ).
).
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72,74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.
Решение. 1) Статистический ряд распределения частот:
| хi | |||||
| пi |
2) Объем выборки: п = 2 + 4 + 8 + 2 + 4 = 20. Найдем относительные частоты, для чего разделим частоты на объем выборки 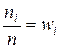 :
:
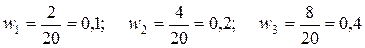 ;
; 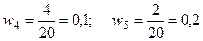
Напишем распределение относительных частот:
| хi | |||||
| wi | 0,1 | 0,2 | 0,4 | 0,1 | 0,2 |
Контроль: 0,1 + 0,2 + 0,4 + 0,1 + 0,2 = 1.
Полигоном частот называют ломаную, отрезки, которой соединяют точки 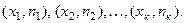 Для построения полигона частот на оси абсцисс откладывают варианты х 2, а на оси ординат – соответствующие им частоты пi. Точки
Для построения полигона частот на оси абсцисс откладывают варианты х 2, а на оси ординат – соответствующие им частоты пi. Точки 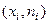 соединяют отрезками и получают полигон частот.
соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки 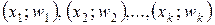 . Для построения полигона относительных частот на оси абсцисс откладывают варианты х i, а на оси ординат соответствующие им частоты w i. Точки
. Для построения полигона относительных частот на оси абсцисс откладывают варианты х i, а на оси ординат соответствующие им частоты w i. Точки 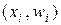 соединяют отрезками и получают полигон относительных частот
соединяют отрезками и получают полигон относительных частот
Пример 2. Постройте полигон частот и полигон относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:
 |
2. Статистический интервальный ряд распределения. Гистограмма.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интерисующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно (или невозможно) учитывать, то варианты группируются в интервалы.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
1. R(размах) = Xmax –Xmin
2. 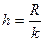 k- число групп
k- число групп
3. 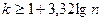 (формула Стерджеса)
(формула Стерджеса)
4. a = xmin, b = xmax
5. 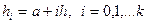
Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
| Интервалы группировки | 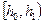 | 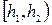 | ... | 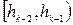 | 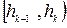 |
| Частоты | 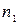 | 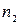 | ... | 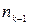 | 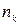 |
Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:
| Интервалы группировки | 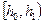 | 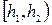 | ... | 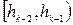 | 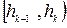 |
| Отн. частоты | 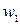 | 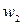 | ... |  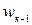 | 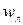 |
 2015-03-22
2015-03-22 26198
26198
