Пример. «Размещения предприятий»

Исходные условия. Пусть в нескольких пунктах расположены предприятия, производящие некоторый продукт. В пунктах размещаются потребители готовой продукции с соответствующими потребностями. Затраты на производство единицы продукта в пункте равны, обьем производства в этом пункте равен, а затраты по транспортировке единицы продукта из i в j равны. Количество перевезенных продуктов из i в j составляет единиц. Уравнения модели:

1.(перевозится неотрицательное количество продукта);

2. (выпускаемое количество продукта не

больше возможного обьема производства и равно вывозимому количеству продукта);

3., j=1,...,n (потребности потребителей),

(каждый пункт потребления получает столько, сколько ему требуется).

Конечная цель. Необходимо получить минимальные затраты на производство и на транспортировку продукции, т.е. обеспечить минимум функции

,

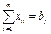
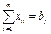
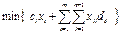
где - затраты на производство,

- затраты на транспортировку.

Целевая функция состоит из аналогичной целевой задачи. Однако, различие состоит в том, что здесь добавляются затраты на производство. Для однотипности подхода к решению этих двух моделей добавляется фиктивный пункт с характеристикой: потребность равна разности между возможным обьемом производства продукта и суммарной потребнос

,

где - затраты на производство,

- затраты на транспортировку.

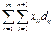Целевая функция состоит из аналогичной целевой задачи. Однако, различие состоит в том, что здесь добавляются затраты на производство. Для однотипности подхода к решению этих двух моделей добавляется фиктивный пункт с характеристикой: потребность равна разности между возможным обьемом производства продукта и суммарной с

Пример Моделирование системы планирования