I. Множества и операции над ними.
1) Для заданных множеств А, В и С найти:
 B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразить на плоскости
B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразить на плоскости 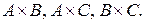 Найти
Найти  считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
2) Для заданного семейства множеств  где Г – заданное индексное множество, найти объединение и пересечение всех множеств семейства, т.е.
где Г – заданное индексное множество, найти объединение и пересечение всех множеств семейства, т.е.  и
и  (по всем возможным индексам
(по всем возможным индексам  ).
).
3) Докажите тождества, используя только определения операций над множествами.
4) Докажите тождество, используя диаграммы Эйлера – Венна.
II. Отношения. Функции. Отношения эквивалентности и упорядоченности.
1) Даны множества  и два бинарных отношения:
и два бинарных отношения:  и
и  . Изобразите Р 1, Р 2 графически. Найдите Р 1-1, Р 2-1,
. Изобразите Р 1, Р 2 графически. Найдите Р 1-1, Р 2-1,  Определите, является ли отношение Р 2 рефлексивным, транзитивным, симметричным, антисимметричным.
Определите, является ли отношение Р 2 рефлексивным, транзитивным, симметричным, антисимметричным.
2) Найдите область определения и область значений отношения Р. Является ли отношение Р рефлексивным, транзитивным, симметричным, антисимметричным?
3) Даны отображения (числовые функции) ƒ, g: ℝ→ℝ. Найти композицию ƒ ◦ g, g ◦ ƒ, обратные отображения: ƒ –1, g -1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найти f (A), g (A), ƒ –1(B), g -1(B). Найти неподвижные точки отображений.
III. Функции и формулы алгебры логики. Эквивалентность формул.
1) Составьте полную и сокращенную таблицы истинности формул.
2) Проверьте двумя способами, будут ли эквивалентны следующие формулы: а) составлением таблиц истинности; б) с помощью эквивалентных преобразований.
3)  Доказать тождественную истинность формулы двумя способами (см. задачу III.2). (Где x
Доказать тождественную истинность формулы двумя способами (см. задачу III.2). (Где x · y = x &Ø y)
IV. Двойственные функции. Принцип двойственности. Совершенные дизъюнктивные, конъюнктивные и полиномиальные нормальные формы (СДНФ, СКНФ, СПНФ – полиномы Жегалкина).
1) Для функций, которые реализуются формулами из задачи III.1, запишите: столбцы значений двойственных функций, СДНФ, СКНФ и СПНФ.
2) Используя принцип двойственности, запишите формулы, двойственные заданным, затем расставьте в полученных формулах скобки, указывающие порядок выполнения действий.
3) С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ, СПНФ.
V. Полные системы функций алгебры логики. Функционально-замкнутые классы.
1) Каким из замкнутых классов Поста принадлежит функция f(x, y, z), заданная своими нулевыми или единичными наборами?
2) Является ли полной система функций? Образует ли она базис?
III. Варианты контрольных работ
Вариант №1
I.1. А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
2.  , где N - множество всех натуральных чисел и
, где N - множество всех натуральных чисел и 

3. 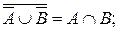 если
если 
4. 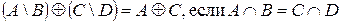
II.1. Р 1 = {(а, 2); (а, 3); (а, 4); (b, 3); (с, 1); (с, 4)}
Р 2 = {(1, 1); (2, 3); (2, 2); (3, 4); (1, 4); (2, 4); (4, 2)}
2. P Í ℝ2 и Р = {(x, y): x · y >1, где x, y Îℝ}
3. f (x) = –(x + 1)2; g (x) = – x –2; А = [–1.5; 1]; В = [–2; –1]
III.1. 
2. x → (y ↓ z) и (x → y) ↓ (x → z)
3. ((x ≡ y) · (x | y)) ≡ x & y
IV.2. 
3. 
V.1. f (0,1,1) = f (0,1,0) = f (1,0,1) = f (1,1,1) =1
2. 
Вариант №2
I.1. А = (0; 10] – полуинтервал на числовой оси
В = [–1; 5] – отрезок числовой оси
С = (–10; 2) – интервал на числовой оси
2.  , где N - множество всех натуральных чисел и
, где N - множество всех натуральных чисел и 

3. 
4. (А \ В)  (В \ С)
(В \ С)  (В \ А)
(В \ А)  (С \ В) = А
(С \ В) = А  С
С
II.1. Р 1 = {(b, 2); (а, 3); (b, 1); (b, 4); (с, 1); (с, 2); (с, 4)}
Р 2 = {(1, 1); (1, 2); (1, 4); (2, 2); (2, 4); (3, 3); (3, 2); (3, 4); (4, 4)}
2. P Í ℝ2 и Р = {(x, y): x 2+ y 2=1, где x, y Îℝ}
3. f (x) = (x + 1)2 – 1; g (x) = x + 1; А = [–1.5; 1]; В = [0; 1]
III.1. 
2. x → (y ≡ z) и (x → y) ≡ (x → z)
3. (x → y) ≡ 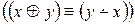
IV.2. 
3. 
V.1. f (0,1,1) = f (0,1,0) = f (1,0,0) = f (1,0,1) =0
2. 
Вариант №3
I.1. А = {0, 1, 2, 3}– четырехэлементное множество
В = [–5; 3] – отрезок числовой оси
С = (0; 2) – интервал на числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 

3. 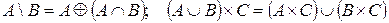
4. (А \ В)  (В \ С)
(В \ С)  (С \ А) = (В \ А)
(С \ А) = (В \ А)  (С \ В)
(С \ В)  (А \ С)
(А \ С)
II.1. Р 1 = {(а, 3); (а, 2); (а, 4); (b 1); (с, 2); (с, 4); (с, 3)}
Р 2 = {(1, 1); (2, 2); (2, 1); (3, 3); (4, 4); (4, 3); (1, 4); (2, 4); (3, 2); (3, 4)}
2. P Í ℝ2 и Р = {(x, y): y =| x |, где x, y Îℝ}
3. f (x) = (x + 1)2 + 1; g (x) = x + 3; А = [–1.5; 1]; В = [2; 3]
III.1. 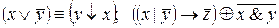
2. x ≡ (y | z) и (x ≡ y) | (x ≡ z)
3. (((x ↓ y)↓(x ↓ y))  ((x ↓ x))↓(y ↓ y))) ≡(x
((x ↓ x))↓(y ↓ y))) ≡(x  y)
y)
IV.2. 
3. 
V.1. f (0,0,1) = f (1,0,0) = f (1,1,0) =1
2. 
Вариант №4
I.1. А = (–1; +∞)– интервал на числовой оси
В = (–10; 10] – полуинтервал на числовой оси
С = [–5; +15] – отрезок числовой оси
2.  , где N - множество всех натуральных чисел и
, где N - множество всех натуральных чисел и 

3. 
4. (А  В)
В)  (С
(С  D) = В
D) = В  С, если А
С, если А  В = D и C
В = D и C  D = A
D = A
II.1. Р 1 = {(b, 1); (а, 3); (а, 4); (с, 2); (с, 4); (b, 4)}
Р 2 = {(1, 1); (2, 3); (2, 2); (2, 4); (3, 3); (3, 4); (4, 2); (4, 4)}
2. P Í ℝ2 и Р = {(x, y): x 2 + x = y 2 + y, где x, y Îℝ}
3. f (x) = (x + 1)2; g (x) = x + 2; А = [–1.5; 1]; В = [1; 2]
III.1. 
2. x ↓ (y | z) и (x ↓ y) | (x ↓ z)
3. (x → z) ≡ ((x 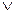 (y & z)) →((x
(y & z)) →((x 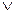 y) & z))
y) & z))
IV.2. 
3. 
V.1. f (0,1,1) = f (1,0,0) = f (1,0,1) =1
2. 
Вариант №5
I.1. А = (–16; 8]– полуинтервал на числовой оси
В = [–9; 9] – отрезок числовой оси
С = (5; +∞) – интервал на числовой оси
2.  , где Γ - множество всех целых чисел за исключением нуля, т.е.
, где Γ - множество всех целых чисел за исключением нуля, т.е.
Γ = {1, –1, 2, –2, 3, –3,…} и 

3. 
4. (А \ (В \ С)) \ ((А \ В)\ С) = А  С
С
II.1. Р 1 = {(а, 2); (а, 4); (b, 1); (b, 2); (b, 4); (с, 2); (с, 4)}
Р 2 = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4); (3, 2); (1, 3); (4, 1)}
2. P Í ℝ2 и Р = {(x, y): x – y  ℤ, где x, y Îℝ}
ℤ, где x, y Îℝ}
3. f (x) = (x – 1)2 – 1; g (x) = x – 1; А = [0.5; 3]; В = [0; 1]
III.1. 
2. x → (y ↓ z) и (x → y) | (x → z)
3. 
IV.2. 
3. 
V.1. f (0,0,0) = f (0,0,1) = f (1,0,0) = f (1,1,0) =0
2. 
Вариант №6
I.1. А = [–25; 1]– отрезок числовой оси
В = {–1; 0; 1} – трехэлементное множество
С = (0; +∞) – интервал на числовой оси
2.  , где Γ - множество всех целых чисел за исключением нуля, т.е.
, где Γ - множество всех целых чисел за исключением нуля, т.е.
Γ = {1, –1, 2, –2, 3, –3,…} и 

3. 
4. (А \ В)  (В \ А) = А
(В \ А) = А  В
В
II.1. Р 1 = {(а, 2); (а, 4); (а, 3); (с, 1); (с, 2); (с, 3)}
Р 2 = {(1, 1); (1, 4); (2, 3); (3, 3); (4, 1); (4, 3); (4, 4)}
2. P Í ℝ2 и Р = {(x, y): x + y = –2, где x, y Îℝ}
3. f (x) = (x – 1)2 + 1; g (x) = x + 1; А = [0.5; 3]; В = [2; 3]
III.1. 
2. x ≡ (y  z) и (x ≡ y)
z) и (x ≡ y)  (x ≡ z)
(x ≡ z)
3. 
IV.2. 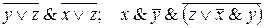
3. 
V.1. f (0,0,1) = f (0,1,1) = f (1,1,0) =0
2. 
Вариант №7
I.1. А = (–10; 5]– полуинтервал на числовой оси
В = [0; 10] – отрезок числовой оси
С = (4; +∞) – интервал на числовой оси
2.  , где Γ - множество всех целых чисел за исключением нуля, т.е.
, где Γ - множество всех целых чисел за исключением нуля, т.е.
Γ = {1, –1, 2, –2, 3, –3,…} и 

3. 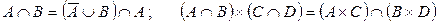
4. ((А  В) \ С) = (А \(В
В) \ С) = (А \(В  С))
С))  (В \(А
(В \(А  С))
С))
II.1. Р 1 = {(а, 1); (b, 2); (b, 3); (с, 1); (с, 3); (с, 4)}
Р 2 = {(1, 1); (1, 2); (1, 3); (2, 2); (2, 3); (3, 3); (3, 4); (4, 1); (4, 4)}
2. P Í ℝ2 и (x, y)  , x, y Îℝ.
, x, y Îℝ.
3. f (x) = (x – 1)2; g (x) = x; А = [0.5; 3]; В = [1; 2]
III.1. 
2. x ↓(y  z) и (x ↓ y)
z) и (x ↓ y)  (x ↓ z)
(x ↓ z)
7. 
IV.2. 
3. 
V.1. f (1,0,0) = f (0,0,1) = f (0,1,1) =0
2. 
Вариант №8
I.1. А = (–∞; 2]– полуинтервал на числовой оси
В = [–3; 3] – отрезок числовой оси
С = (0; 4) – интервал на числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 
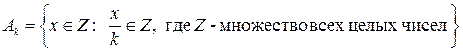
3. 
4. 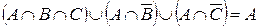
II.1. Р 1 = {(а, 3); (b, 4); (b, 3); (с, 1); (с, 2); (с, 4)}
Р 2 = {(1, 2); (1, 3); (1, 4); (2, 3); (4, 3); (4, 2)}
2. P Í ℝ2, (x, y)  и x, y Îℝ.
и x, y Îℝ.
3. f (x) = – (x + 1)2 –1; g (x) = x– 1; А = [–1.5; 1]; В = [–3; –2]
III.1. 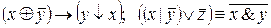
2. x 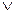 (y
(y  z) и (x
z) и (x 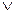 y)
y)  (x
(x 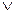 z)
z)
3 
IV.2. 
3. 
V.1. f (0,0,1) = f (0,1,1) = f (1,0,0) = f (1,0,1)=1
2. 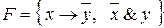
Вариант №9
I.1. А = (–2; 3) – интервал на числовой оси
В = [0; 4] – отрезок числовой оси
С = {2; 3} – двухэлементное множество
2.  , где ℕ – множество всех натуральных чисел и
, где ℕ – множество всех натуральных чисел и 

3. 
Если 
4. 
II.1. Р 1 = {(а, 3); (b, 4); (b, 3); (b, 1); (b, 2); (c, 2)}
Р 2 = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 3); (4, 2)}
2. P Í ℝ2, (x, y) 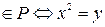 , где x, y Îℝ.
, где x, y Îℝ.
3. f (x) = 1– (x + 1)2; g (x) = x+ 1; А = [–1.5; 1]; В = [–1; 0]
III.1. 
2. x → (y ≡ z) и (x → y) ≡ (x → z)
3. 
IV.2. 
3. 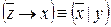
V.1. f (1,0,0) = f (0,1,1) = f (0,1,0) =0
2. 
Вариант №10
I.1. А = [–7.5; 4.5]– отрезок числовой оси
В = (0; 5)– интервал на числовой оси
С = (–10; 0] – полуинтервал на числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 
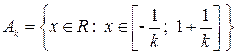
3.  ;
;

4. 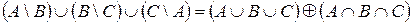
II.1. Р 1 = {(а, 2); (а, 3); (a, 4); (b, 1); (b, 2); (b, 4)}
Р 2 = {(1, 1); (1, 3); (1, 4); (2, 2); (2, 3); (3, 2); (3,3); (4,3); (4,4)}
2. P Í ℝ2, (x, y)  , где x, y Îℝ.
, где x, y Îℝ.
3. f (x) = – (x – 1)2 –1; g (x) = x– 3; А = [0.5; 3]; В = [–3; –2]
III.1. 
2. x → (y | z) и (x → y) | (x → z)
3. 
IV.2. 
3. 
V.1. f (1,0,1) = f (0,1,1) = f (0,1,0) =0
2. 
Вариант №11
I.1. А = (–5; 5]– полуинтервал на числовой оси
В = (0; +∞)– интервал на числовой оси
С = {–1; 0; 1} – трехэлементное множество
2.  , где ℕ- множество всех натуральных чисел и
, где ℕ- множество всех натуральных чисел и 

3. 
 где U – универсальное множество
где U – универсальное множество
4. 
II.1. Р 1 = {(а, 1); (а, 2); (b, 3); (b, 4); (c, 3); (c, 4)}
Р 2 = {(1, 1); (1, 4); (2, 1); (2, 2); (2, 4); (3, 3)}
2.  , (x, y)
, (x, y) 
3. f (x) = 1– (x – 1)2; g (x)= x –1; А = [0.5; 3]; В = [–1; 0]
III.1. 
2. x | (y  z) и (x | y)
z) и (x | y)  (x | z)
(x | z)
3. 
IV.2. 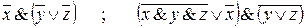
3. 
V.1. f (0,0,0) = f (0,0,1) = f (1,0,0) = f (1,1,0) =1
2. 
Вариант №12
I.1. А = (–12; 12)– интервал на числовой оси
В = [10; 20] – отрезок числовой оси
С = (–∞; +15] - полуинтервал на числовой оси
2.  , где ℕ – множество всех натуральных чисел и
, где ℕ – множество всех натуральных чисел и 

3. 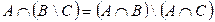

4. 
II.1. Р 1 = {(а, 2); (а, 3); (а, 4); (с, 3); (c, 1); (c, 4)}
Р 2 = {(1, 4); (2, 3); (2, 1); (3, 4); (4, 2)}
2.  , (x, y)
, (x, y) 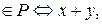 кратно 3.
кратно 3.
3. f (x) = – (x – 1)2; g (x)= x; А = [–1.5; 1]; В = [–2; –1]
III.1. 
2. 
3. 
IV.2. 
3. 
V.1. f (0,0,0) = f (0,1,0) = f (1,1,1) =0
2. 
Вариант №13
I.1. А = (5; 15] – полуинтервал на числовой оси
В = [5; 10] – отрезок числовой оси
С = {4; 5; 6} – трехэлементное множество
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 
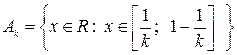
3.  если
если  Æ
Æ
если 
4. 
II.1. Р 1 = {(а, 1); (а, 2); (а, 4); (b, 2); (b, 4); (c, 3)}
Р 2 = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4);(4,2)}
2.  , (x, y)
, (x, y)  кратно 2
кратно 2
3. f (x) = – (x – 1)2; g (x)= x – 2; А = [0.5; 3]; В = [–2; –1]
III.1. 
2. 
3. 
IV.2. 
3. 
V.1. f (0,0,0) = f (0,0,1) = f (1,1,0) =0
2. 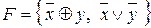
Вариант №14
I.1. А = (0; + ∞) – интервал на числовой оси
В = [–3; 3] – отрезок числовой оси
С = (–10; 0] - полуинтервал на числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 

3. 

4. 
II.1. Р 1 = {(b, 1); (b, 3); (c, 1); (c, 2); (c, 3); (c, 4)}
Р 2 = {(1, 1); (2, 2); (2, 3); (2, 4); (3, 2); (3, 3); (3, 4); (4, 2); (4, 3); (4, 4)}
2.  , (x, y)
, (x, y) 
3. f (x) = (x+ 1)2–1; g (x)= – x – 1; А = [–1.5; 1]; В = [0; 1]
III.1. 
2. 
3. 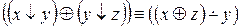
IV.2. 
3. 
V.1. f (0,0,1) = f (0,1,1) = f (1,1,1) =0
2. 
Вариант №15
I.1. А = [–5; 25) – полуинтервал на числовой оси
В = [–25; 5] – отрезок числовой оси
С = (–10; 15) - интервал на числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 

3. 
Если 
4. 
II.1. Р 1 = {(a, 2); (a, 4); (b, 3); (c, 1); (c, 2)}
Р 2 = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 4); (4, 3); (4, 2)}
2.  , (x, y)
, (x, y) 
3. f (x) = (x+ 1)2 +1; g (x)= 1– x; А = [–1.5; 1]; В = [2; 3]
III.1. 
2. 
3. 
IV.2. 
3. 
V.1. f (0,0,1) = f (1,0,0) = f (1,1,0) =0
2. 
Вариант №16
I.1. А = (0; 25) – интервал на числовой оси
В = {0; 1; 2} – трехэлементное множество
С = [–1; 1] - отрезок числовой оси
2.  , где ℕ - множество всех натуральных чисел и
, где ℕ - множество всех натуральных чисел и 

3. 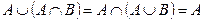

4. 
II.1. Р 1 = {(а, 3); (а, 2); (b, 2); (b, 3); (c, 1); (c, 4)}
Р 2 = {(1, 1); (1, 2); (2, 2); (3, 3); (4, 1); (4, 4)}
2.  , (x, y)
, (x, y) 
3. f (x) = (x – 1)2 –1; g (x)= 1 – x; А = [0.5; 3]; В = [0; 1]
III.1. 
2. 
3. 
IV.2. 
3. 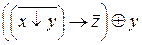
V.1. f (0,1,1) = f (1,0,0) = f (1,0,1) =0
2. 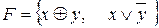
Вариант №17
I.1. А = [–7; 7] – отрезок числовой оси
В = [0; +∞) – полуинтервал на числовой оси
С = (–∞; 5) - интервал на числовой оси
2.  , где ℕ– множество всех натуральных чисел и
, где ℕ– множество всех натуральных чисел и 
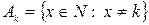
3. 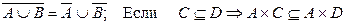
4. 
II.1. Р 1 = {(а, 1); (а, 2); (а, 4); (b, 3); (c, 1); (c, 4)}
Р 2 = {(1, 3); (1, 2); (2, 3); (3, 2); (3, 4); (4, 1)}
2.  , (x, y)
, (x, y) 
3. f (x) = (x – 1)2 +1; g (x)= 3 – x; А = [0.5; 3]; В = [2; 3]
III.1. 
2. 
3. 
IV.2. 
3. 
V.1. f (1,0,0) = f (1,1,0) = f (0,1,1) = f (0,1,0) =1
2. 
Вариант №18
I. 1. А =[–  ; 3) – полуинтервал на числовой оси
; 3) – полуинтервал на числовой оси
В =[3; 10] – отрезок числовой оси
С =(3; +  ) – интервал на числовой оси
) – интервал на числовой оси
2. {А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 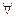

 ℝ
ℝ
A  = { x
= { x  ℝ: x
ℝ: x  }
}
3. (A 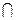 B) \ C =(A \ C)
B) \ C =(A \ C) 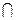 (B \ C)
(B \ C)
(A  B)
B)  (C
(C  D)
D)  (A
(A  C)
C)  (B
(B  D)
D)
4. (A  (A \ B))
(A \ B)) 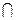
 = Æ
= Æ
II. 1. P 1={ (a, 1); (b, 3); (c; 1); (c, 4); (c, 3); (c, 2)}
 P 2={(1, 1); (1, 2); (1, 4); (2, 1); (2, 2); (2, 3); (3, 3); (3, 2); (3, 4); (4, 3); (4, 4); (4, 1)}
P 2={(1, 1); (1, 2); (1, 4); (2, 1); (2, 2); (2, 3); (3, 3); (3, 2); (3, 4); (4, 3); (4, 4); (4, 1)}
2. P  ℤ2, (x, y)
ℤ2, (x, y)  P
P  x = – y
x = – y
3. f (x)=(x +1)2; g (x)= – x; A =[–1.5; 1]; B = [1; 2]
III. 1. (х 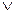 y)
y)  (y
(y  ); (x
); (x 
 )
)  (z |
(z |  )
)
2. x 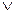 (y
(y  z) и (x
z) и (x 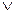 y)
y)  (x
(x 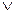 z)
z) 
3. (((x | y)  (y
(y 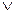 z))
z))  (z
(z 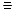 t))
t)) 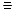 ((t
((t · z) · y)
IV. 2. ((x 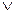 y) &(
y) &( )
) 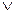
 );
); 
3. 
V. 1. f (1,0,1) = f (0,1,0) = f (1,1,1) = 0
2. F ={ x 
 ,
,  }
}
Вариант №19
I. 1. А =[–11; 11] –отрезок числовой оси
В =[–12; 3) – полуинтервал на числовой оси
С =(0; 12) – интервал на числовой оси
2. { А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 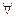

 ℝ
ℝ
A  = { x
= { x  ℝ: x
ℝ: x  }
}
3. A \ (B 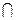 C) = (A \ B)
C) = (A \ B)  (A \ C); (A \ B)
(A \ C); (A \ B)  C = (A
C = (A  C) \ (B
C) \ (B  C)
C)
4. ((A  C)
C)  (B
(B  D))
D)) 
II. 1. P 1={(a, 1); (b, 3); (b, 1); (b, 4); (c, 3); (c, 2)}
 P 2={(1, 3); (1, 4); (2, 2); (3, 3); (4, 3); (4, 4);}
P 2={(1, 3); (1, 4); (2, 2); (3, 3); (4, 3); (4, 4);}
2. P  ℤ2, (x, y)
ℤ2, (x, y)  P
P  x +1 = y
x +1 = y
3. f (x)=(x – 1)2; g (x)=2– x; A =[0.5; 3]; B =[1; 2]
III. 1. 
2. 
3. 
IV. 2. 
3. 
V. 1. f (0,0,0) = f (1,0,1) = f (1,1,1) = 0
2. F ={ x 
 , x
, x 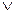 y }
y }
Вариант №20
I. 1. А =(–10; 1) –интервал на числовой оси
В ={–1; 0; 1} – трехэлементное множество
С =[0.5; 10] – отрезок числовой оси
2. { А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 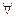

 ℝ
ℝ
A  = { x
= { x  ℝ: x2
ℝ: x2  2}
2}
3. 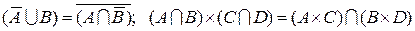
4. 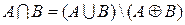
II. 1. P 1={(a, 1); (a, 2); (a; 4); (b, 1); (b, 4); (c, 3)}
 P 2={(1, 1); (2, 4); (2, 1); (3, 3); (4, 2); (4, 1)}
P 2={(1, 1); (2, 4); (2, 1); (3, 3); (4, 2); (4, 1)}
2. P  ℤ2, (x, y)
ℤ2, (x, y)  P
P  y ≥ x – 2
y ≥ x – 2
3. f (x)= – x 2 – 1; g (x)= – x – 3; A =[–0.5; 2]; B =[–3; –1]
III. 1 
2. 
3. 
IV. 2. 
3. 
V.1. f (0,0,1) = f (0,1,1) = f (1,1,0) = f (1,1,1)= 1
2. F = 
Вариант №21
I. 1. А =[10; 20] – отрезок числовой оси
В =(0; 15) – интервал на числовой оси
С ={5; 10; 15} – трехэлементное множество
2. { А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 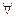

 ℝ
ℝ
A  = { x
= { x  ℝ: x 2 <
ℝ: x 2 <  2}
2}
3. 
4. 
II. 1. P 1={(a, 1); (a, 4); (b, 2); (b, 3); (c, 1); (c, 4)}
 P 2={(1, 1); (1, 4); (2, 1); (3, 4); (4, 3); (4, 1)}
P 2={(1, 1); (1, 4); (2, 1); (3, 4); (4, 3); (4, 1)}
2. P Í ℕ2, (x, y)  P
P  НОД (x, y) ≠ 1 (НОД– наибольший общий делитель)
НОД (x, y) ≠ 1 (НОД– наибольший общий делитель)
3. f (x)= 1– x 2; g (x)= – x – 1; A =[–0.5; 2]; B =[–1; 0]
III. 1 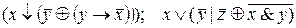
2. 
3. 
IV. 2. 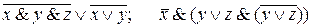
3. 
V. 1. f (0,0,0) = f (1,1,1) = f (1,1,0) = 0
2. F = {  }
}
Вариант №22
I. 1. А = {–1; 0; 1} – трехэлементное множество
В =(–10; 0.5) – интервал на числовой оси
С =[0; 10] – отрезок числовой оси
2. { А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 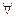

 ℝ
ℝ
A  = { x
= { x  ℝ: x 2 ≥
ℝ: x 2 ≥  2+1}
2+1}
3. 
4. 
II. 1. P 1={(a, 1); (a, 2); (b, 2); (b, 4); (c, 3); (c, 2)}
 P 2={(1, 1); (1, 2); (2, 2); (3, 3); (4, 3); (4,4)}
P 2={(1, 1); (1, 2); (2, 2); (3, 3); (4, 3); (4,4)}
2. P Í ℕ2, (x, y)  P
P  x ≠ y
x ≠ y
3. f (x)= – x 2; g (x)= – x – 2; A =[–0.5; 2]; B =[–2; –1]
III. 1. 
2. 
3. 
IV. 2. 
3. 
V. 1. f (0,0,1) = f (1,1,1) = f (1,1,0) = 0
2. F ={ 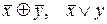 }
}
Вариант №23
I. 1. А = [–6; +6) - полуинтервал
В =[–10; 2] –отрезок
С =(2; 10) – интервал
2. { А  }
} 
 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 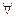

 ℝ
ℝ
A  = { x
= { x  ℝ: x 2 <
ℝ: x 2 <  2 +1}
2 +1}
3. 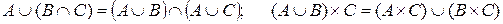
4. 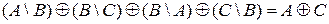
II. 1. P 1={(a, 1); (a, 2); (a, 4); (c, 3); (c, 2); (c, 4)}
 P 2={(2, 1); (3, 1); (3, 2); (4, 1); (4, 3)}
P 2={(2, 1); (3, 1); (3, 2); (4, 1); (4, 3)}
2. P Í ℕ2, (x, y)  P
P  x 2 = y
x 2 = y
3. f (x)= x 2; g (x)= 2– x; A =[–0.5; 2]; B =[1; 2]
III. 1. 
2. 
3. 
IV. 2. 
3.
 2015-10-22
2015-10-22 2065
2065








