Из результатов наблюдений

Если в полученной группе результатов наблюдений одно или два существенно отличаются от остальных, а наличия ошибки в снятии показаний и других промахов не обнаружено, то необходимо проверить, не являются ли они грубыми погрешностями, подлежащими исключению. Решение этой задачи выполняется общими методами проверки статистических гипотез в предположении нормального распределения результатов наблюдений. Проверяемая гипотеза состоит в утверждении, что результат 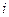-го наблюдения 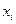не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдения рассматривают как грубую погрешность и его исключают.

Рассмотрим методику использования одного из критериев, рекомендуемого государственным стандартом.

Критерий оценки анормальности результатов наблюдений при неизвестном СКО .

При исключении по этому критерию грубых погрешностей из результатов проводят следующие операции:

1. Результаты группы из наблюдений, называемые объемом выборки, упорядочивают по возрастанию . Вычисляют оценки среднего арифметического значения и СКО наблюдений этой выборки. Для предполагаемых промахов, которыми, например, могут быть и , проводят расчет коэффициентов: , .

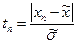2. Задаются уровнем значимости критерия ошибки 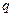. Очевидно, этот уровень должен быть достаточно малым, чтобы вероятность ошибки была невелика.

3. Из таблицы предельных значений коэффициента по заданным параметрам 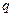и находят предельное (граничное) значение коэффициента.

Число наблюдений n	Предельное значение при уровне значимости q	Число наблюдений n	Предельное значение при уровне значимости q
0,100	0,075	0,050	0,025	0,100	0,075	0,050	0,025
	1,15	1,15	1,15	1,15		2,13	2,20	2,29	2,41
	1,42	1,44	1,46	1,48		2,17	2,24	2,33	2,47
	1,60	1,64	1,67	1,72		2,21	2,28	2,37	2,50
	1,73	1,77	1,82	1,89		2,25	2,32	2,41	2,55
	1,83	1,88	1,94	2,02		2,28	2,35	2,44	2,58
	1,91	1,96	2,03	2,13		2,31	2,38	2,48	2,62
	1,98	2,04	2,11	2,21		2,34	2,41	2,50	2,66
	2,03	2,10	2,18	2,29		2,36	2,44	2,53	2,68
	2,09	2,14	2,29	2,36		2,38	2,46	2,56	2,71

4. Выполняют сравнение коэффициентов, определяемых по вышеприведенным формулам. Если и , то результаты и исключают из результатов наблюдений.

С уменьшением коэффициента значимости 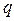коэффициент при том же числе наблюдений увеличивается. Это означает, что при снижении 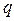все меньшее число результатов наблюдений может быть отнесено к промахам. Поэтому слишком малые значения 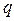не используют.

Критерий «трех сигм»

Данный критерий применяется для результатов измерений, распределенных по нормальному закону, и одним из граничных параметров служит оценка СКО измерений . По этому критерию считается, что результат, полученный с вероятностью 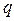<0,003. маловероятен, и его можно считать промахом, если 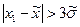, при этом значения и вычисляют без учета экстремальных значений 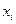. Данный критерий достаточно хорош при .