Оценка 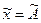 измеряемой величины
измеряемой величины  является случайной величиной и отличается от нее на некоторую абсолютную погрешность
является случайной величиной и отличается от нее на некоторую абсолютную погрешность  . В связи с этим представляет интерес определение доверительного интервала (
. В связи с этим представляет интерес определение доверительного интервала ( ), в котором с заданной доверительной вероятностью
), в котором с заданной доверительной вероятностью  находится измеряемая величина
находится измеряемая величина  .
.
В доверительном интервале  погрешности
погрешности  называются доверительными границами случайной погрешности результата измерения, а
называются доверительными границами случайной погрешности результата измерения, а  и
и 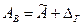 - нижней и верхней границей доверительного интервала.
- нижней и верхней границей доверительного интервала.
Аналитически доверительная вероятность записывается в виде:

Границы доверительного интервала (доверительные границы) указываются обычно симметричными относительно результата измерения. В более общем случае может быть задан и несимметричный доверительный интервал  .
.
С целью единообразия представления случайных погрешностей при технических измерениях доверительная вероятность принимается равной 0,95. лишь для особо точных измерений допускается использовать более высокую доверительную вероятность.
Если число наблюдений n велико, то для расчета доверительной границы  можно использовать нормальный закон распределения. При числе наблюдений менее 20 наиболее точный расчет
можно использовать нормальный закон распределения. При числе наблюдений менее 20 наиболее точный расчет  получается при использовании распределения Стьюдента.
получается при использовании распределения Стьюдента.
При использовании нормального закона поиск доверительного интервала выполняется с помощью интеграла вероятностей 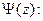
| z | Ψ(z) | z | Ψ(z) | z | Ψ(z) | z | Ψ(z) |
| 0,00 | 0,000 | 0,70 | 0,516 | 1,40 | 0,839 | 2,25 | 0,976 |
| 0,10 | 0,080 | 0,80 | 0,576 | 1,50 | 0,866 | 2,50 | 0,988 |
| 0,20 | 0,159 | 0,90 | 0,632 | 1,60 | 0,890 | 2,75 | 0,994 |
| 0,30 | 0,236 | 1,00 | 0,683 | 1,70 | 0,911 | 3,00 | 0,9973 |
| 0,40 | 0,311 | 1,10 | 0,729 | 1,80 | 0,928 | 3,30 | 0,9990 |
| 0,50 | 0,383 | 1,20 | 0,770 | 1,90 | 0,943 | 3,50 | 0.9995 |
| 0,60 | 0,452 | 1,30 | 0,806 | 2,00 | 0,955 | 4,00 | 0.9999 |
Задаваясь доверительной вероятностью  =
= 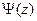 , по таблице находят
, по таблице находят  . Затем, учитывая СКО
. Затем, учитывая СКО  , определяют доверительную границу случайной погрешности результата измерений
, определяют доверительную границу случайной погрешности результата измерений 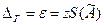 .
.
Аналитически нижнюю и верхнюю границы доверительного интервала записывают в виде:
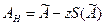 и
и  .
.
 2015-10-22
2015-10-22 765
765








