Основные определения и теоремы

Неориентированный граф с числом вершин n>1 называется деревом, если он связен и не содержит циклов.

Следующая теорема характеризует свойства деревьев, каждое из которых может служить определением дерева.

Теорема 1. Для графа G, имеющего n вершин (n>1), равносильны следующие свойства:

1. G связен и не содержит циклов;

2. G не содержит циклов и имеет (n-1) ребро;

3. G связен и имеет (n-1) ребро;

4. G не содержит циклов, но добавление ребра между любыми его вершинами приводит к образованию цикла;

5. G связен, и все его ребра являются перешейками;

6. Всякая пара вершин G соединена только одной цепью.

Доказательство этой теоремы можно провести, показав цепочку следствий 1 2 3 4 5 6 1.

Доказательство. Если граф G связен и не имеет циклов, то цикломатическое число ν=N-n+1=0, откуда N=n-1, т.е. G не содержит циклов и имеет (n-1) ребро (1 2).

Если G не имеет циклов, то ν=0, причем N=n-1, т.е.
ν = N – n + P = 0, откуда получаем P=1, т.е. G связен и имеет (n-1) ребро (2 3).

Если G связен и имеет (n-1) ребро, то ν = N – n + 1, N = n - 1. Отсюда ν=0, т.е. G не содержит циклов. Если добавить одно ребро, получим связной граф G’ с числом ребер N’=n. Цикломатическое число этого графа ν’=n-n+1=1, т.е. G’ содержит один цикл(3 4).

Если G не содержит циклов, но добавление одного ребра ведет к образованию цикла, то G связен, так как в противном случае в графе G должны существовать две вершины x_i и x_j, не соединенные никакой цепью и такие, что добавление ребра (x_i x_j) не привело бы к образованию цикла. Все ребра графа G являются перешейками, т.к. удаление любого из них приводит к графу G’, для которого ν’=N-n+P=0, причем N’=N-1. Так как G связен и не содержит циклов, ν’=N-n+1=0, откуда N=n-1, N’=n-2 и, следовательно, P=2. Т.е. G’ не является связным (4 5).

Если G связен, то всякая пара его вершин соединена цепью. В силу того, что все ребра G являются перешейками, существует единственная цепь, соединяющая любую пару вершин x_i, x_j, т.к. в противном случае удаление ребра (x_i x_j) не нарушило бы связности графа G (5 6).

Если всякая пара вершин G соединена цепью, то G связен. Так как такая цепь единственная, G не содержит циклов: если бы G содержал циклы, то в нем нашлась бы пара вершин x_i, x_j, соединенная более чем одной цепью (6 1), что и требовалось доказать.

Ориентированное дерево называется прадеревом.

Несвязный граф, компонентами связности которого являются деревья, называется лесом.

В дальнейшем понадобится следующее определение: подграф G’(X’,U’), содержащий все вершины графа G(X,U), называется частичным графом.

Теорема 2. Граф G(X,U) тогда и только тогда содержит частичный граф, являющийся деревом, когда он связен.

Доказательство. Если граф G содержит частичный подграф-дерево, то, очевидно, он связен, т.к. на основе свойства 6 предыдущей теоремы каждая пара его вершин может быть соединена цепью.

Предположим теперь, что граф связен. Докажем, что он содержит частичный граф-дерево.

Если граф G не содержит циклов, то он сам является деревом по определению. Предположим, что G содержит цикл μ. Вычеркнем из μ любое ребро. Получившийся частичный граф G₁ будет связным, т.к. удаление из цикла любого ребра не нарушает связности графа. Если G₁ – дерево, доказательство закончено. Если G₁ содержит циклы, то удаляем ребро любого из них и получаем подграф G₂ . Если G₂ не имеет циклов, то он есть дерево и доказательство закончено. Если G₂ содержит циклы, то удаляем ребро одного из них, и т.д.

Через несколько шагов получим связной граф без циклов, т.е. дерево, являющееся подграфом исходного графа G.

Постановка задачи

Предположим, что имеется n городов, которые нужно соединить нефтепроводом (электролинией, газопроводом). Стоимость строительства нефтепровода между городами x_i, x_j задана. Как построить самый дешевый нефтепровод, связывающий все города?

Построим граф, вершинами которого обозначены города, а ребрами возможные нефтепроводы между ними. Каждому ребру графа (x_i,x_j) поставим в соответствие число l (x_i,x_j)≥0, равное стоимости строительства нефтепровода на участке (x_i,x_j). Задача строительства самого дешевого нефтепровода сводится к следующей задаче на графе. Задан конечный неориентированный связной граф G(X,U) каждому ребру которого (x_i,x_j)=u_k, u_k 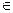U, поставлено в соответствие число l (u_k)≥0, называемое длинной ребра. Требуется найти такой частичный граф-дерево графа G (частичное дерево), общая длина ребер которого минимальна. Решение этой задачи может быть получено с помощью следующего алгоритма.

Алгоритм Краскала

Алгоритм построения кратчайшего дерева для графа G(X,U) состоит в следующем:

1. Выбираем самое короткое ребро графа u₁, затем ребро u₂, самое короткое из оставшихся;

2. Из оставшихся ребер выбираем самое короткое ребро u₃ так, чтобы оно не образовывало цикла с выбранными ребрами;

3. Продолжаем эту процедуру. На k-м шаге к выбранным ребрам u_1,…,u_к-1 добавляем самое короткое ребро из оставшихся │U│-(к-1) ребер так, чтобы оно не образовывало цикла с выбранными ребрами;

4. При k=n-1 процесс заканчивается. Получим граф без циклов с (n-1)-м ребром. На основании теоремы 1 (пункт 2) построенный граф есть дерево, обозначим его T(n-1).

Докажем, что построенное по этому графу дерево T(n-1) кратчайшее.

1. Сначала предположим что G – полный граф, и длины всех его ребер различны. Для доказательства воспользуемся методом от противного. Предположим, что построенное T(n-1) дерево не кратчайшее и имеется отличное от него кратчайшее дерево T. В этом случае существуют две возможности:

а) T и Т(n-1) не имеют общих ребер. Присоединим к дереву Т ребро u₁Є Т(n-1). В этом случае согласно пункту 4 теоремы 1 в получившемся графе имеется цикл, одним из ребер которого является u₁. Выбросим из этого цикла любое ребро u’≠u₁.В результате этой операции получим частичное дерево Т', которое отличается от Т одним ребром: u’ заменено u₁. Но l (u₁) < l (u'), т.к. u₁ – кратчайшее ребро. Следовательно, l (T') < l (T) т.е. Т не кратчайшее дерево;

б) Т и Т(n-1) имеют общие ребра u₁, u₂,…, u_(k-1). Пусть u_к есть первое ребро, принадлежащее Т(n-1), но не принадлежащее Т.

Рассмотрим граф, который получится присоединением к дереву Т ребра u_к, т.е. 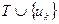. В соответствии с пунктом 4 теоремы 1 в нем есть цикл μ, причем μ содержит ребро u’, не принадлежащее Т(n-1), т.к. в противном случае дерево Т(n-1) содержало бы цикл, что противоречит определению дерева.

Удалив из цикла μ ребро u’, получим дерево 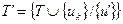, отличающееся от Т одним ребром: u' заменено на u_k. Но l(u_k)< l (u’), т.к. в противном случае на k-м шаге при построении дерева Т(n-1) в него включили бы ребро u’. Следовательно, l (Т')< l (Т) т.е. Т – не кратчайшее дерево.

2. Пусть G(X,U)- неполный граф, но его ребра имеют разную длину. Пусть l (U)=L –сумма длин всех ребер графа G. Присоединим к G столько новых ребер, сколько требуется для получения полного графа. Припишем каждому вновь построенному ребру длину l _j>L.

В полученном полном графе построим кратчайшее дерево Т(n-1).

На основании теоремы 2 в графе G есть кратчайшее дерево, длина которого не превосходит L. Частичное дерево графа G будет являться частичным деревом для построенного полного графа. Поэтому ни одно новое ребро в кратчайшее дерево входить не может. Следовательно, для построения кратчайшего частичного дерева в графе G можно пользоваться алгоритмом Краскала.

3. Предположим теперь, что некоторые ребра графа G(X,U) имеют одинаковую длину. Пусть Δ – минимальная ненулевая разность длин ребер. Обозначим 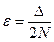, где N=│U│. Пусть l ₁,…, l _m – все значения длин ребер графа; k_j ребер принимают значение l_j. Занумеруем ребра графа в порядке увеличения длины. Затем изменим длину ребра графа следующим образом: 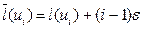. В получившемся графе длины всех ребер различны. Выберем с помощью алгоритмов Краскала кратчайшее частичное дерево. Проведенное изменение длин ребер графа обладает тем свойством, что если в исходном графе , то и в графе с ребрами измененной длины 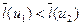. Следовательно, кратчайшее частичное дерево в новом графе будет кратчайшим и в старом.

В графе, где некоторые ребра имеют одинаковую длину, кратчайшее частичное дерево может не быть однозначно определенным.

Пример

Требуется построить газопровод, соединяющий 10 городов (рис. 3.2.1.). Возможные соединения городов обозначены ребрами, длины которых l (x_i, x_j), представляющие собой стоимость строительства газопровода на участке (x_i, x_j), заданы и обозначены на графе. Как построить самый дешевый газопровод?

Задача сводится к отысканию частичного дерева заданного графа, общая длина ребер которого минимальна. Воспользуемся алгоритмом Краскала.

Частичное дерево должно содержать (n-1) ребер, т.е. 9. Общее число ребер исходного графа .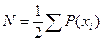

Рис. 3.2.1

Заданные длины ребер удобно поместить в следующую симметричную таблицу, в которой достаточно заполнить один из углов – верхний или нижний по отношению к главной диагонали (рис.3.2.2). На пересечении строки x_i и столбца x_j стоит число, равное длине дуги (x_i,x_j), т.е. l (x_i,x_j). Число заполненных клеток равно числу ребер графа. Следуя алгоритму, выбираем самые короткие ребра u₁=(x₁,x₂), u₂=(x₄,x₆), l (u₁)= l (u₂)=1.

Рис. 3.2.2

Отметим это, зачеркнув выбранные числа в таблице и пометив выбранные ребра на графе жирной чертой. Наименьшее из оставшихся чисел в таблице есть 2, т.е. длина дуги (x₁,x₃). Выбираем в качестве u₃ ребро (x₁,x₃), т.к. оно не образует цикла с выбранными ребрами. Вновь делаем отметку в таблице и на графе и т.д. Получим в результате u₄=(x₉,x₁₀), u₅=(x₁,x₁₀), u₆=(x₄,x₅), u₇=(x₂,x₅), u₈=(x₈,x₁₀), u₉=(x₇,x₆).

Длина последнего выбранного ребра равна 9, т.к. ребра графа с меньшими длинами не могут являться ребрами дерева. Сумма длин ребер построенного дерева L=34. Стоимость строительства самого дешевого газопровода по исходным данным составляет 34 денежные единицы.