Теорема 5.4.2. Если в некоторой окрестности точки а(или при достаточно больших значениях х) функция заключена между двумя функциями и, имеющими одинаковый предел А при, то функция имеет тот же предел А.
Пусть при 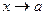
 ,
, 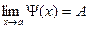 . Это означает, что для любого
. Это означает, что для любого 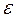 >0 найдется такое число
>0 найдется такое число >0, что для всех
>0, что для всех 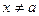 и удовлетворяющих условию
и удовлетворяющих условию 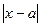 <
< будут верны одновременно неравенства
будут верны одновременно неравенства
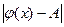 <
<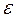 ,
, 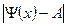 <
<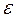
или
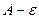 <
<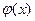 <
<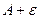 ,
, 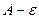 <
<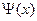 <
<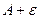 .
.
Пусть 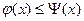 . Так как по условию функция
. Так как по условию функция 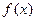 заключена между двумя функциями
заключена между двумя функциями
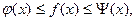
то из неравенств следует, что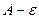 <
<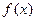 <
<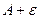 , т.е.
, т.е. 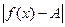 <
<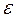 .
.
А это означает, что 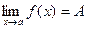 ,(рис.5.4.2)
,(рис.5.4.2)
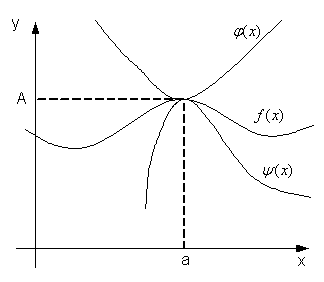
Рис.5.4.2
Пусть 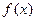 и
и 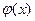 - функция, для которых существуют пределы при
- функция, для которых существуют пределы при 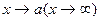 :
: 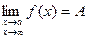 ,
, 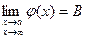 .
.
Сформулируем основные теоремы о пределах.
1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
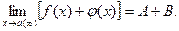 (5.4.3)
(5.4.3)
2. Предел произведения конечного числа функций равен произведению пределов этих функций
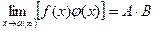 (5.4.4)
(5.4.4)
В частности, постоянный множитель можно выносить за знак предела:
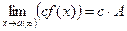
3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю):
 (5.4.5)
(5.4.5)
4. Если 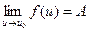 ,
, 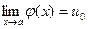 , то предел сложной функции
, то предел сложной функции
 (5.4.6)
(5.4.6)
Докажем в качестве примера свойство 5.4.4. По условию 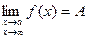 и
и 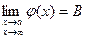 , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функций в соответствии с формулой
, следовательно, на основании теоремы о связи бесконечно малых величин с пределами функций в соответствии с формулой 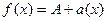 ,
, 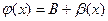 , где а (х) и
, где а (х) и 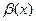 - бесконечно малые величины при
- бесконечно малые величины при 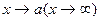 . Перемножая почленно оба неравенства, получаем
. Перемножая почленно оба неравенства, получаем
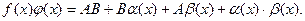
На основании свойств бесконечно малых последние три слагаемых представляют бесконечно малую величину 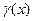 при
при 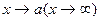 . Итак, функция
. Итак, функция 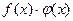 представляет сумму постоянного числа А·В и бесконечно малой
представляет сумму постоянного числа А·В и бесконечно малой 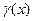 . На основании обратной теоремы о связи бесконечно малых величин с пределами функции это означает, что
. На основании обратной теоремы о связи бесконечно малых величин с пределами функции это означает, что 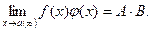
Замечание. В теоремах о пределах предполагается существование пределов функций 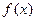 и
и 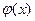 , из чего следует заключения о значениях пределов суммы, произведения или частного функций. Но из существования предела суммы, произведения или частного функций еще не следует, что существуют пределы самих слагаемых, сомножителей или делимого и делителя.
, из чего следует заключения о значениях пределов суммы, произведения или частного функций. Но из существования предела суммы, произведения или частного функций еще не следует, что существуют пределы самих слагаемых, сомножителей или делимого и делителя.
Например, 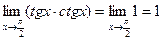 , но отсюда еще не следует существования пределов
, но отсюда еще не следует существования пределов 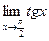 и
и  . И действительно, в данном случае первого из этих пределов не существует.
. И действительно, в данном случае первого из этих пределов не существует.
Теоремы 5.4(1,2,3,4) не имеют места, если требования, указанные в этих теоремах, не выполняются.
Пусть  ,
, 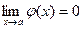 ,
, 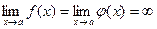 при вычислении пределов сумм, произведений, частного можно прийти к выражениям вида
при вычислении пределов сумм, произведений, частного можно прийти к выражениям вида 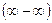 ,
, 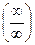 ,
, 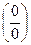 ,
, 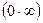 ,
, 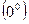 ,
, 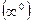 ,
, 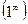 . Такие выражения называются неопределенными(неопределенностями). Вычисление пределов в таких случаях сводится к раскрытию неопределенностей путем различных преобразований. Например, пусть
. Такие выражения называются неопределенными(неопределенностями). Вычисление пределов в таких случаях сводится к раскрытию неопределенностей путем различных преобразований. Например, пусть 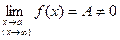 и
и 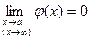 .
.
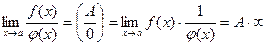 (
(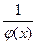 - бесконечно большая).
- бесконечно большая).
Примеры. Вычислить пределы.
1. 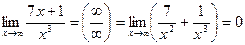 (свойства бесконечно малых).
(свойства бесконечно малых).
2. 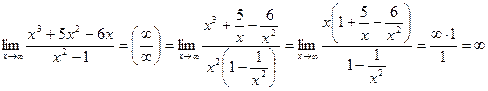
3.
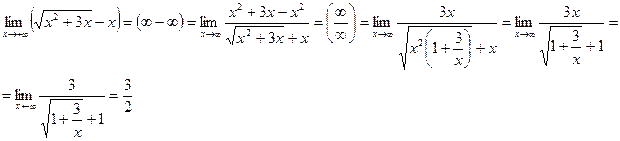
Были использованы теоремы о пределах и свойства бесконечно малых величин.
 2014-02-05
2014-02-05 2813
2813








