Задача о кротчайшем пути между двумя вершинами
ориентированного графа и ее экономическая
интерпретация
Постановка задачи
Постановка задачи состоит в следующем. Задан конечный ориентированный граф G(x,гx), или G(x,u). Каждой дуге графа «u» поставлено в соответствие некоторое число l(u)³0, называемое длинной дуги «u». Длинной пути m называется сумма длин дуг, составляющих данный путь.
 .
.
Требуется для двух фиксированных вершин xo и xn графа G(x,u) найти самый короткий соединяющий их путь.
К данной задаче может быть сведена следующая задача экономического содержания. Задана сеть дорог, соединяющих пункты xi (i=0,1,…,n). Найти путь, соединяющий пункты xo и xn, по которому можно доставить груз в кратчайшее время. При этом время доставки груза из пункта xi в xj (i,jÎ0,…,n) задано и равно l (uij)= l (xi,xj)³0.
Если под длинной дуги l (xi,xj) понимать стоимость перевозки груза из пункта xi в xj, то содержание задачи составит определение такого пути из пункта xi в xj, на котором затраты на транспортировку были бы минимальными.
Пример.
Имеем 6 пунктов Х (x0,…,x6). Сеть дорог, связывающих эти пункты, изображена на графе (рис.3.3.1).
Время доставки груза из i-го пункта в j-й, т.е. l (xi,xj), задано и изображено числом в кружке, записанным рядом с дугой (xi,xj). Так, l (x0,x1)=2, l (x0,x2)=4, l (x0,x3)=5, l (x1,x4)=3 и т.д.

Рис. 3.3.1
Требуется определить путь, по которому из пункта x0 в пункт x5 можно доставить груз в кратчайшие время, и само кратчайшее время доставки.
Итак, задача о кратчайшем пути между двумя фиксированными вершинами ориентированного графа предполагает, во-первых, определение длины кратчайшего пути, во-вторых, определение самого кратчайшего пути.
Алгоритм
Алгоритм решения этой задачи позволяют определить кратчайший путь и его длину за конечное число шагов. Каждая вершина графа получает некоторую числовую метку на первом шаге. Затем метки, вообще говоря, могут меняться, становясь на некотором шаге постоянным числом. Установившаяся метка данной вершины есть кратчайшее расстояние от этой вершины до вершины x0. Если пути, соединяющего x0 и xn, не существует, будем считать длину кратчайшего пути между этими вершинами равной + 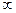 .
.
Алгоритм состоит в последовательном выполнении следующих операций:
1. На первом шаге ставим следующие метки: для вершины x0:l0=0, для любой другой вершины xi lj=+ 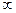 (i=1,…,n);
(i=1,…,n);
2. Ищем на графе такую дугу (xi,xj), для которой lj-li> l (xi,xj). Причем разность 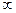 -
- 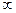 считаем равной 0. Если такая дуга найдется, меняем метку вершины xj на
считаем равной 0. Если такая дуга найдется, меняем метку вершины xj на 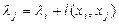 . Если такой дуги не найдется, то пути, соединяющего x0 с xn, не существует, т.к. из x0 ни в какую другую вершину графа не идет ни одна дуга.;
. Если такой дуги не найдется, то пути, соединяющего x0 с xn, не существует, т.к. из x0 ни в какую другую вершину графа не идет ни одна дуга.;
3. Повторяем процедуру пункта 2 до тех пор, пока метки вершин не перестанут меняться.
Установившиеся метки обозначим l*i (i=1,2,…,n). При этом может быть два случая:
1) l*n=+ 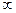 .
.
Это значит, что пути, соединяющего x0 и xn, не существует. Длина кратчайшего пути равна + 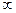 .
.
2) l*n – конечное число.
Оно равно кратчайшему расстоянию между вершинами x0 и xn.
Кратчайший путь получаем следующим образом. Ищем вершину 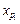 такую, что
такую, что 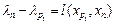 , затем
, затем  , для которой
, для которой  и т.д. до тех пор, пока не придем в вершину
и т.д. до тех пор, пока не придем в вершину 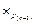 = x0. Путь, проходящий через отмеченные вершины
= x0. Путь, проходящий через отмеченные вершины  , является кратчайшим.
, является кратчайшим.
Как следует из построения и правил изменения меток, метки вершины xi (i=1,…,n) могут меняться конечное число раз (метка вершины x0 l0=0 не меняется), т.к. конечная метка всякой вершины равна длине некоторого пути из x0 в данную вершину xi.
Из построения следует, что отмеченный путь
m ( ) – есть кратчайший путь. В самом деле, пусть существует другой путь
) – есть кратчайший путь. В самом деле, пусть существует другой путь  из вершины x0 в xn, проходящий через вершины x0, y1, y2, …, yr, xn. Из построения следует, что
из вершины x0 в xn, проходящий через вершины x0, y1, y2, …, yr, xn. Из построения следует, что

Складывая эти неравенства и учитывая, что  = 0, получим
= 0, получим  , т.е.
, т.е.  . Заметим, что решение задачи может не быть однозначным, т.е. существует несколько путей минимальной длины из вершины x0 в xn.
. Заметим, что решение задачи может не быть однозначным, т.е. существует несколько путей минимальной длины из вершины x0 в xn.
Рассмотренный алгоритм известен в литературе как алгоритм Форда.
Решение данной задачи можно ускорить, сократив число шагов, если пользоваться формулой
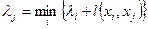 . (3.3.1)
. (3.3.1)
Задача об отыскании кратчайшего пути между двумя вершинами ориентированного графа может быть решена методами целочисленного программирования. Решение по приведенному алгоритму является более простым.
Обратимся к приведенному выше примеру. Определим кратчайший путь, соединяющий пункты x0 и x5. При этом будем пользоваться формулой (3.3.1)
Для вершины x0 полагаем l0=0. Для всех остальных вершин li=+ 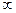 (i=1…,5). Затем ищем дугу, для которой lj-l0> l (x0,xj). Начнем с вершины x1.
(i=1…,5). Затем ищем дугу, для которой lj-l0> l (x0,xj). Начнем с вершины x1.
l1-l0= 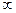 > l (x0,x1)=2.
> l (x0,x1)=2.
Следовательно, меняем метку вершины x1 на
l’1=l0+ l (xo,x1)=2.
Аналогично определяем метку вершины X2
l’2=l0+ l (xo,x2)=4.
Чтобы найти изменившуюся метку вершины x3, следует воспользоваться формулой (3.3.1), т.к. в вершину x3 направлены две дуги, идущие из двух разных верши x0 и x1:
| l’3=min{[l’1+ l (x1,x3)],[ l0+ l (x0,x3)]}=min{(2+4),(0+5)}=5. | (xo) |
Аналогично определяем новые метки для вершин x4 и x5:
| l’4=min{[l’1+ l (x1,x4)],[ l’3+ l (x3,x4)]}=min{(2+3),(5+6)}=5, | (x1) |
| l’5=min{[l’2+ l (x2,x5)],[l’3+ l (x3,x5)],[l’4+ l (x4,x5)]}= =min{(4+7),(5+4),(5+2)}=7. | (x4) |
В данном случае получили установившиеся метки вершин на втором шаге (на первом шаге полагали l0=0, li=+ 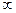 ). Каждая из меток l’j – длина кратчайшего пути из вершин xi в данную вершину xj. Длина кратчайшего пути из x0 в x5 есть
). Каждая из меток l’j – длина кратчайшего пути из вершин xi в данную вершину xj. Длина кратчайшего пути из x0 в x5 есть
l*5=l’5=7.
При подсчете значений l’j справа в скобках отмечены вершины, по которым достигается минимум. Так, для x5 l’5=7, если прийти в эту вершину из вершины x4, т.е. l’5=l’4+ l (x4,x5). Метка для вершины x5 примет большее значение, если прийти в x5 из x2 или x3. Следовательно, кратчайший путь в x5 проходит через вершину x4 (p1=4 в приведенных выше обозначениях). В x4 он идет через вершину x1 (p2=1), в x1 из x0 (p3=р4=0). Итак, кратчайший путь из вершины x0 в x5 проходит через вершины x0,x1,x4,x5. Искомый путь m есть (x0,x1,x4,x5); l (m)=7.
В рассмотренном примере установившиеся метки получили за один шаг, потому что, воспользовавшись формулой (3.3.1), определили кратчайший путь между входом и выходом графа-сети. Заметим, что для графов-сетей кратчайший путь между входом и выходом графов всегда существует. Причем он может быть получен за один шаг без предварительного изменения меток, т.е. алгоритм становится совсем простым, если пользоваться формулой (3.3.1) и правильной нумерацией вершин графа, что и было проделано в этой задаче.
Сети. Отношение порядка между вершинами
ориентированного графа
Ориентированный граф без циклов, имеющий одну вершину без входящих дуг (вход графа) и одну вершину без выходящих дуг (выход графа), называется сетью.
Отыскание экстремальных путей на графах такого вида используется в различных экономических расчетах. К их числу относятся рассмотренная выше задача, а также задачи сетевого планирования.
В любом ориентированном графе без циклов можно установить отношение порядка между его вершинами.
Вершина xi предшествует вершине xj,  , если существует дуга из xi в xj. Это отношение порядка удовлетворяет аксиомам порядка:
, если существует дуга из xi в xj. Это отношение порядка удовлетворяет аксиомам порядка:
1) если xi предшествует xj, то xj не предшествует xi;
2) если xi предшествует xj, а xj предшествует xk, то xi предшествует xk.
«Правильная» нумерация вершин графа заключается в том, что если xi предшествует xj, то номера i и j должны удовлетворять неравенству i<j.
На графе-сети практически это можно сделать, используя распределение вершин по рангам методом вычерчивания дуг. Вычеркиваем дуги, исходящие из входа графа, вершины x0. Вершины, соответствующие концам этих дуг и не имеющие после этой операции входящих дуг, относим к вершинам I-го ранга. На графе G (рис.3.3.1) вершинами I-го ранга являются вершины x1 и x2. Вершины I-го ранга получают первые порядковые номера 1,2. Внутри одного ранга нумерация произвольна.
Затем вычеркиваем дуги, выходящие из вершин I-го ранга. Вершины, соответствующие концам таких дуг и не имеющие после этих операций входящих дуг, относим к вершинам 2-го ранга. Они получают следующие порядковые номера. В нашем примере к вершинам 2-го ранга относится одна вершина x3.
Процесс вычеркивания дуг продолжается до тех пор, пока все вершины графа не будут занумерованы. Последний порядковый номер получит вершина xn – выход графа.
В рассмотренном примере все вершины распределены по 4 рангам. К вершинам 3-го ранга принадлежит x4, а к вершинам 4-го ранга – x5.
Существуют и другие способы «правильной» нумерации вершин графа, в том числе алгоритм Форда для нумерации вершин графа.
Задача о пути максимальной длины между двумя
вершинами ориентированного графа
в сетевом планировании
Постановка задачи
Задача ставится следующим образом.
Задан конечный ориентированный граф без контуров G(x,u).
Каждой дуге графа «u» ставится в соответствие длина дуги l(u).
Требуется определить длиннейший путь, соединяющий две вершины графа x0 и xn.
Аналогичные задачи можно ставить для ориентированных графов с контурами, а также неориентированных графов. Но в этом случае во избежание бессодержательности задачи нужно вводить дополнительные условия, исключающие пути бесконечной длины.
Решение задачи состоит как в отыскании пути максимальной длинны между двумя фиксированными вершинами графа, так и в определении величины этого пути.
Одну из основных задач сетевого планирования составляет отыскание путей максимальной длины между входом и выходом графа-сети.
Алгоритм
Каждая вершина графа получает числовую метку, которая может меняться конечное число раз. Установившаяся метка – величина длиннейшего пути из вершины x0 в данную вершину xj. В частности, установившаяся метка вершины xn есть величина длиннейшего пути из x0 в xn.
Чтобы определить искомый путь, нужно рассмотреть последовательность шагов, на каждом из которых ищется одна из дуг длиннейшего пути между x0 и xn.
Алгоритм состоит в последовательном проведении следующих этапов:
1. Полагаем λ0 = 0; λi = -∞ (i = 1,…,n).
2. Ищем дугу (xi, xj) такую, что 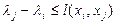 . Если такой дуги нет, то не существует пути, соединяющего x0 и xn. Если такая дуга найдется, то изменяем метку lj на l’j=lj +
. Если такой дуги нет, то не существует пути, соединяющего x0 и xn. Если такая дуга найдется, то изменяем метку lj на l’j=lj +
+ l(x0,xj).
3. Продолжаем процедуру пункта 2 до тех пор, пока метки вершин xi не перестанут меняться.
Установившиеся метки обозначим l*i. При этом могут встретиться два случая:
1) l*n= - 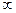 , это соответствует тому, что пути, соединяющего вершины x0 и xn, не существует;
, это соответствует тому, что пути, соединяющего вершины x0 и xn, не существует;
2) l*n- конечное число. Оно равно длине пути максимальной длины из x0 в xn.
Сам путь находим, отмечая вершины, по которым достигается максимум, т.е. те вершины, для которых
 .
.
Если между вершинами графа-сети установлено отношение порядка, т.е. они «правильно» занумерованы, то решение задачи можно получить за один шаг, произведя подсчет меток с учетом следующей формулы:
 . (3.3.2)
. (3.3.2)
Пример.
Определим длиннейший путь на графе, изображенном на рис.3.3.1, а также его длину.
Вначале полагаем для вершины x0 l0=0 и lj=- 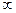 для вершин xi (i=1,…,5).
для вершин xi (i=1,…,5).
Затем, т.к. l1-l0=- 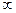 < l (x0,x1), меняем метку вершины x1, т.е. l1, на
< l (x0,x1), меняем метку вершины x1, т.е. l1, на
| l’1=l0+ l (x0,x1)=2. | (x0) |
Аналогично l’2=l0+ l (x0,x2)=4.
Чтобы найти метку вершины x3, пользуясь формулой (3.3.2)
| l’3=max{[l’1+ l (x1,x3)],[l0+ l (x0,x3)]}=max{(2+4),(0+5)}=6. | (x1) |
Справа в скобках отмечаем вершины, по которым достигается максимум длины.
Аналогично
| l’4=max{[l’1+ l (x1,x4)],[ l’3+ l (x3,x4)]}=max{(2+3),(6+6)}=12, | (x3) |
| l’5=max{[l’3+ l (x3,x5)],[l’4+ l (x4,x5)],[l’2+ l (x2,x5)]= =max{(6+4),(12+2),(4+7)}=14. | (x4) |
Искомый путь имеет длину l (m)=l*5=14. Причем в x5 он идет из вершины x4, в x4 из x3, в x3 из x1, в x1 из x0: x5,x4,x3,x1,x0. Следовательно, m=(x0,x1,x3,x4,x5).
Путь максимальной длины называют критическим путем. Следовательно, критический путь в рассмотренном примере есть m=(x0,x1,x3,x4,x5), а его длина l (m)=14.
Сетевое планирование. Скорейшее время
завершения проекта
Рассмотрим некоторый проект – совокупность операций (работ), составляющий некоторый многошаговый процесс. Примером может служить строительство некоторого объекта. Считаем известными все работы, которые предстоит совершить, их последовательность и время, необходимое для выполнения каждой работы. Проект может быть изображен в виде графа-сети. Зададимся целью определить кратчайший срок завершения проекта.
Пусть данные о строительстве приведены в следующей таблице
| Виды работ | Какие работы следуют за перечисленными | Продолжительность работ |
| 2,3 | ||
| 6,7 | ||
| 6,7 | ||
| – | ||
| – | ||
| – |
Эту информацию о проекте представим в виде графа-сети. Дугами графа будем изображать работы, а вершинами графа – некоторые события. Назовем элементарными событиями начало и конец каждой работы, а некоторую совокупность элементарных событий – событием.
Вход графа – событие, заключающееся в начале всего проекта. Оно является событием, стоящим в начале одной или нескольких работ, а именно тех, которые не следуют ни за какими другими, т.е. работ, с которых может быть начато строительство. В нашем примере такими работами являются №1,4,5 (их нет во 2-ом столбце).
Выходом графа будет являться событие, заключающееся в окончании работ, за которыми не следуют никакие другие работы, т.е. в окончании всего проекта. В данном примере – это работы №7,8,9.
Все другие вершины графа есть события, заключающиеся в окончании одних и начале других работ.
Сетевой граф, соответствующий приведенным в таблице данным, изображен на рис. 3.3.2. Номер работы обозначен числом вне кружка. Число, обведенное кружком, есть продолжительность данной работы. Вход графа, вершина x0 – начало проекта. Выход графа, вершина x5 – окончание проекта.

Рис. 3.3.2
Вершины x1,x2,x3,x4 есть события, заключающиеся в начале одних и окончании других работ. Так, например, вершина x3 есть окончание 3-й и 4-й работ и начало 6-й и 7-й.
Путь максимальной длины из вершины x0 в xi есть скорейшее время наступления события xi. В самом деле, событие x3, например, соответствующее началу 6-й и 7-й работ, может произойти только после окончания 3-й и 4-й работ, а следовательно, и после окончания 1-й, т.к. для выполнения 3-й работы необходимо окончание 1-й работы. Следовательно, скорейшее время наступления события x3 есть
max{5,(2+4)}=6.
Скорейшее время наступления события 5 есть скорейшее время окончания проекта в целом и равно длине пути максимальной длины из вершины x0 в x5.
Итак, если x0 и xn есть вход и выход графа-сети, соответствующего данному проекту, то для определения наиболее раннего срока окончания всех работ нужно найти путь максимальной длины из x0 в xn, т.е. критический путь, и определить его длину. Время, соответствующее скорейшему окончанию работ, т.е. скорейшему завершению проекта, называется критическим временем данного проекта. Оно численно совпадает с длиной критического пути из x0 в xn.
В приведенном примере критический путь, проходящий через вершины x0,x1,x3,x4,x5, имеет длину, равную 14 l (m)=14, т.е. критическое время данного проекта равно 14.
Работы, составляющие критический путь, называются критическими работами (операциями). От своевременного выполнения критических операций зависит срок завершения проекта. Они не допускают запаздывания в исполнении в отличие от некритических операций.
С другими параметрами сетевого графа, правилами составления графа-сети, а также вопросами сетевого планирования в целом читатель может ознакомиться по списку литературы.
1. Как определить граф?
2. Какова геометрическая реализация ориентированного, неориентированного, смешанного графа?
3. Каковы свойства матрицы смежности графа? Можно ли с помощью матрицы смежности задать граф?
4. Как построить матрицу инцидентности графа?
5. Как построить матрицу достижимости?
6. Что такое граф-сеть?
7. Какова формула связи между количеством рёбер графа и степенями вершин графа?
8. Какой граф называется связным? Не связным? Какое ребро называется перешейком?
9. Как определяется граф-дерево?
10. Когда граф содержит Эйлеров цикл? Эйлерову цепь?
11. Каков алгоритм построения Эйлерова цикла и Эйлеровой цепи на графе?
12. Существует ли алгоритм построения Гамильтонова цикла на графе?
13. Как найти объединение двух графов?
14. Как найти пересечение двух графов?
15. Как найти граф, являющийся прямым произведением графов?
16. Как провести операции объединения, пересечения графов, заданных матрицами смежности?
17. Как определить число внутренней устойчивости графа?
18. Как определить число внешней устойчивости графа?
19. Как определить цикломатическое число?
20. Как определить хроматическое число графа?
21. Какова формула связи между количеством вершин графа и числами внутренней устойчивости и хроматическим числом графа?
22. Какие графы называются изоморфными?
23. Какой граф называется плоским?
24. Какие графы называются гомеоморфными?
25. Каково достаточное условие планарности графа?
26. Как формулируется и решается задача о четырёх красках?
27. Чему равно цикломатическое число графа дерева?
28. Если «n» – количество вершин графа-дерева, то чему равно количество его рёбер?
29. Любые ли вершины графа-дерева можно соединить цепью?
30. Что станет с графом-деревом, если удалить любое ребро?
31. Что станет с графом-деревом, если любые его вершины соединить ещё одним ребром?
32. Сколько компонент связности имеет граф-дерево?
33. Как определяется «частичное дерево»?
34. В чём состоит алгоритм Краскала?
35. В чём отличие всех последующих шагов алгоритма Краскала от первого шага?
36. Что является завершающим шагом алгоритма Краскала и почему?
37. Какой смысл имеют метки вершин xi в алгоритме Форда?
38. Метка какой вершины не меняется во всех итерациях?
39. При определении кратчайшего пути между двумя фиксированными вершинами ориентированного графа. Как влияет использование формулы на решение задачи.
40. Когда кратчайший путь между двумя фиксированными вершинами ориентированного графа определяется за один шаг, не считая нулевой итерации?
41. В каких экономических задачах применяется алгоритм Форда для отыскания кратчайшего пути между двумя фиксированными вершинами ориентированного графа?
42. Какие метки получают вершины графа в нулевой итерации и какой смысл они имеют при определении длиннейшего пути между двумя фиксированными вершинами ориентированного графа?
43. При определении длиннейшего пути между двумя фиксированными вершинами ориентированного графа. Как влияет на решение задачи использование формулы.
44. Когда длиннейший путь между двумя фиксированными вершинами ориентированного графа определяется за один шаг, не считая нулевой итерации?
45. Каков алгоритм метода правильной нумерации вершин сетевого графа путём вычёркивания дуг, какие номера получат вершины одного ранга?
46. Какие номера получат вход и выход графа при правильной нумерации вершин сетевого графа?
47. В чём состоит основная идея сетевого планирования? Опишите краткое содержание задачи?
48. Какую смысловую нагрузку имеют вершины и дуги графа в сетевом планировании?
49. Как построить граф-сеть по заданной таблице последовательности работ, составляющих данный проект?
50. С каких работ заданного проекта нужно начинать строительство графа-сети?
51. Почему длина пути максимальной длины из x0 в вершину xj есть кратчайшее время наступления события xj?
52. Как определяется критический путь и критическое время сетевого графа?
 2015-10-22
2015-10-22 2117
2117

