Теоремы о пределах. 1. Предел суммы конечного числа функций равен сумме пределов этих функций, т.е

1. Предел суммы конечного числа функций равен сумме пределов этих функций, т.е.

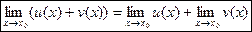
2. Предел произведения конечного числа функций равен произведению их пределов, т.е.

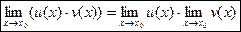
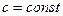Следствие. Если , то .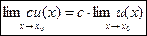

3. Предел частного равен частному пределов

,

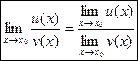если предел знаменателя не равен нулю .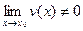

Пример 6.16. Используя теоремы о пределах, найдите

.

.

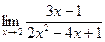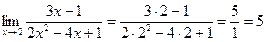Пример 6.17. Используя теоремы о пределах, найдите

.

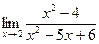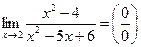. Имеем неопределённость. «Раскроем» эту неопределённость (т.е. избавимся от неё), разложив числитель и знаменатель на множители и сократив их далее на общий множитель :

.

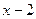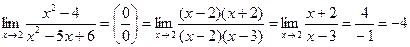Пример 6.18. Используя теоремы о пределах, найдите

.

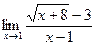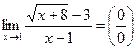. Имеем неопределённость. Домножим числитель и знаменатель дроби на выражение, сопряжённое к числителю:

.

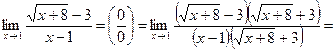
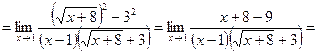
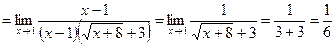Замечательные пределы

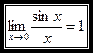(6.1)

, (6.2)

где 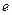— иррациональное число, .

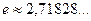Пример 6.19. Найдите .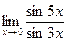

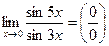. Имеем неопределённость. Поделим числитель и знаменатель дроби под знаком предела на 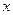и воспользуемся первым замечательным пределом (формула (6.1)):

.

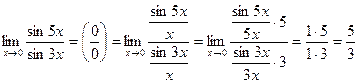Пример 6.20. В п.3 §2 была приведена формула вычисления конечной величины начальной суммы через лет в случае, если удельная процентная ставка есть , а проценты начисляются 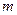раз в году. Вычислим сумму 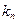, если начисление процентов происходит непрерывно, т.е. .

=

=

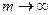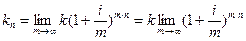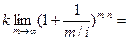
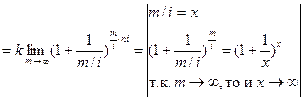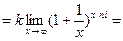(в силу (6.2)) = .

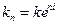§ 3. Непрерывность функции.

Функция 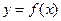называется непрерывной в точке 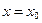, если .

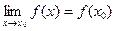Данное определение требует выполнения следующих условий:

v Функция 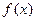определена в точке 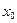и некоторой её окрестности;

v Пределы слева и справа существуют и равны между собой ;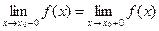

v .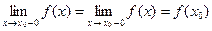

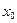Если в точке не выполняется хотя бы одно из указанных условий, то эта точка 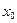называется точкой разрыва функции.

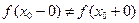В случае, когда , но эти пределы конечные, то точку 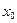называют точкой разрыва первого рода. (См., например, рис.1 §3).

Если хотя бы один из пределов 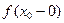или 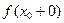не существует или равен бесконечности, то 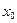называется точкой разрыва второго рода.

Величина 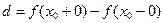называется скачком функции в точке разрыва .

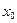Если функция непрерывна во всех точках отрезка 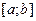, то она называется непрерывной на этом отрезке.

Из определения непрерывности функции и теорем о пределах следуют теоремы:

Сумма конечного числа непрерывных функций в точке 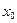непрерывна в этой точке.

Произведение конечного числа непрерывных функций в точке 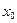непрерывно в этой точке.

Частное двух непрерывных функций непрерывно в тех точках 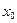, в которых знаменатель отличен от нуля.

Сложная функция, составленная из непрерывных функций, непрерывна в соответствующей точке.

Всякая элементарная функция непрерывна в каждой точке, в которой она определена.