1. Предел числовой последовательности.
2 Числовой последовательностью называется бесконечное множество чисел 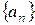 , каждое из которых является значением некоторой функции
, каждое из которых является значением некоторой функции 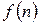 натурального аргумента (
натурального аргумента (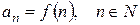 ). При этом
). При этом 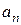 называется членом последовательности, а n – его номером.
называется членом последовательности, а n – его номером.
Пределом числовой последовательности 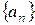 при n, стремящемся к бесконечности, называют такое число А, к которому неограниченно приближаются члены последовательности при неограниченном росте номера n. Дадим более точное определение предела числовой последовательности с использованием известных нам кванторов.
при n, стремящемся к бесконечности, называют такое число А, к которому неограниченно приближаются члены последовательности при неограниченном росте номера n. Дадим более точное определение предела числовой последовательности с использованием известных нам кванторов.
2 Число A называют пределом числовой последовательности 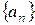 при n, стремящемся к бесконечности (
при n, стремящемся к бесконечности (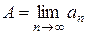 ), если для любого
), если для любого 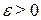 найдется такой номер
найдется такой номер 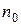 , начиная с которого (т.е. при всех натуральных
, начиная с которого (т.е. при всех натуральных 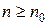 ) будет выполнено неравенство
) будет выполнено неравенство 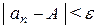 . Или
. Или
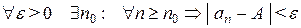 .
.
2Говорят, что 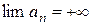 если
если
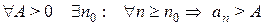 .
.
Примерно аналогично можно сформулировать определение предела в том случае, когда он равен минус бесконечности. Предоставляем это читателям.
Произвольная последовательность может стремиться к конечному или бесконечному пределу, или совсем не иметь предела при 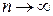 . Рассмотрим три примера.
. Рассмотрим три примера.
Ø Докажем, что 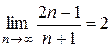 . Для этого для любого числа
. Для этого для любого числа 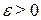 достаточно указать такой номер
достаточно указать такой номер 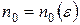 , начиная с которого (т.е. при
, начиная с которого (т.е. при 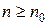 ) будет выполнено неравенство
) будет выполнено неравенство 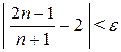 . Решим данное неравенство относительно n:
. Решим данное неравенство относительно n: 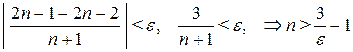 . Следовательно, в качестве
. Следовательно, в качестве 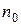 можно выбрать любое натуральное число, превосходящее
можно выбрать любое натуральное число, превосходящее 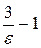 . Например, можно взять целую часть числа
. Например, можно взять целую часть числа 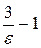 плюс единица (
плюс единица (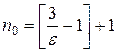 ).
).
Ø Докажем, что 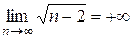 . Для этого достаточно для любого числа
. Для этого достаточно для любого числа 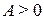 указать такой номер
указать такой номер 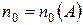 , начиная с которого (т.е. при
, начиная с которого (т.е. при 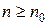 ) будет выполнено неравенство
) будет выполнено неравенство 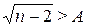 . Решим данное неравенство относительно n:
. Решим данное неравенство относительно n: 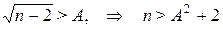 . Следовательно
. Следовательно 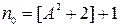 , где под символом […], как и в предыдущем примере, обозначается целая часть действительного числа.
, где под символом […], как и в предыдущем примере, обозначается целая часть действительного числа.
Ø Последовательность 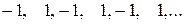 с общим членом
с общим членом 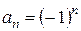 вообще не имеет никакого предела. Действительно, с одной стороны члены последовательности ограничены (
вообще не имеет никакого предела. Действительно, с одной стороны члены последовательности ограничены (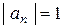 ), и, следовательно, предел последовательности
), и, следовательно, предел последовательности 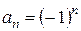 не может быть равен плюс или минус бесконечности. С другой стороны, он не может быть равен никакой константе А. Действительно, какое бы мы не взяли число А, существуют члены последовательности со сколь угодно большими номерами, отличающиеся от А не меньше, чем на 1.
не может быть равен плюс или минус бесконечности. С другой стороны, он не может быть равен никакой константе А. Действительно, какое бы мы не взяли число А, существуют члены последовательности со сколь угодно большими номерами, отличающиеся от А не меньше, чем на 1.
2. Предел функции.
2.Число А называется пределом функции y = f (x) при x, стремящемся к x 0, если для любого e > 0 существует такое d > 0, что для любого x ¹ x 0, удовлетворяющего неравенству | x – x 0 | < d, выполнено неравенство | f (x) – А | < e. Или, сокращенно, 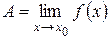 , если
, если
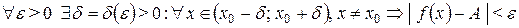 .
.
В качестве упражнения сформулируйте определения предела в тех случаях, когда переменная x стремится к 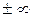 , или предел равен
, или предел равен 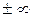 .
.
2 Если 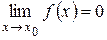 , то функция
, то функция 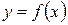 называется бесконечно малой величиной при
называется бесконечно малой величиной при 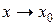 .
.
g Теорема 4.1. Пусть 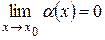 и
и 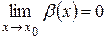 , тогда
, тогда 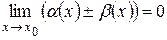 (сумма или разность двух бесконечно малых величин является бесконечно малой величиной).
(сумма или разность двух бесконечно малых величин является бесконечно малой величиной).
4 Пусть e – произвольное положительное число. Тогда из условия теоремы следует, что для выбранного e
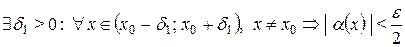 (4.1)
(4.1)
и
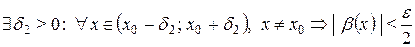 . (4.2)
. (4.2)
Таким образом, если для любого e > 0 выбрать 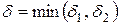 , то из неравенств (4.1) и (4.2) будет следовать, что
, то из неравенств (4.1) и (4.2) будет следовать, что
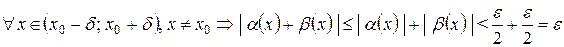 .
.
Следовательно, 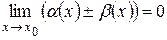 . 3
. 3
Аналогично доказываются теоремы:
1 Теорема 4.2. Если 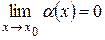 и с – некоторая константа, то
и с – некоторая константа, то
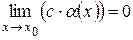 (произведение бесконечно малой величины на константу является бесконечно малой величиной).
(произведение бесконечно малой величины на константу является бесконечно малой величиной).
1 Теорема 4.3. Пусть 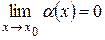 и
и 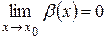 , тогда
, тогда 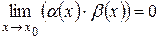 (произведение двух бесконечно малых величин является бесконечно малой величиной).
(произведение двух бесконечно малых величин является бесконечно малой величиной).
g Теорема 4.4. Если 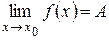 , где А – некоторая константа, то разность
, где А – некоторая константа, то разность 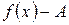 является бесконечно малой величиной.
является бесконечно малой величиной.
4 Из условия теоремы следует, что
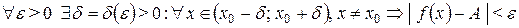 .
.
Переписывая последнее неравенство в виде 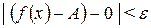 , мы получим, что
, мы получим, что 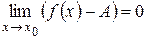 . 3
. 3
g Теорема 4.5. Если 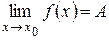 ,
, 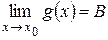 , где А и В – некоторые константы, то
, где А и В – некоторые константы, то 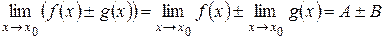 .
.
4 Из теоремы 4.4 следует, что 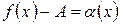 и
и 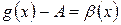 ,
,
где 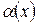 и
и 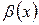 – бесконечно малые величины. Тогда
– бесконечно малые величины. Тогда
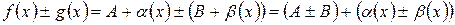 .
.
Но, в соответствии с теоремой 4.1, функция 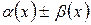 является бесконечно малой величиной. Следовательно,
является бесконечно малой величиной. Следовательно, 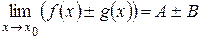 . 3
. 3
g Теорема 4.6. Если 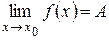 ,
, 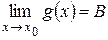 , где А и В – некоторые константы, то
, где А и В – некоторые константы, то 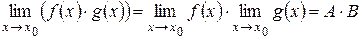 .
.
4 Из теоремы 4.4 следует, что 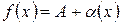 и
и 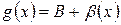 ,
,
где 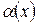 и
и 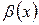 – бесконечно малые величины. Тогда
– бесконечно малые величины. Тогда
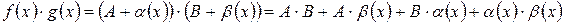 .
.
В соответствие с теоремами 4.2 и 4.3 выражения 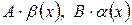 и
и 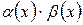 являются бесконечно малыми величинами. Следовательно,
являются бесконечно малыми величинами. Следовательно,
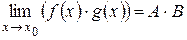 . 3
. 3
Аналогично доказываются следующие утверждения:
1 Теорема 4.7. Если 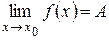 ,
, 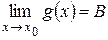 , где А и В – некоторые константы, причем В ¹ 0, то
, где А и В – некоторые константы, причем В ¹ 0, то 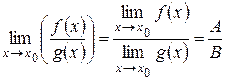 .
.
1 Теорема 4.8. Если 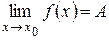 ,
, 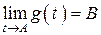 , то
, то
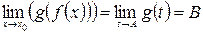 .
.
1 Теорема 4.9. Пусть 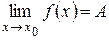 , и
, и 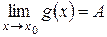 , и пусть существует такая функция
, и пусть существует такая функция 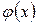 и такое d > 0, что для любого x ¹ x 0, удовлетворяющего неравенству | x – x 0 | < d выполнено неравенство
и такое d > 0, что для любого x ¹ x 0, удовлетворяющего неравенству | x – x 0 | < d выполнено неравенство 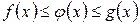 . Тогда
. Тогда 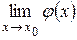 существует и равен А.
существует и равен А.
 2015-04-01
2015-04-01 893
893








