Среднее значение любой периодической функции f(t) за период Т равно:
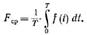
Для синусоидальной функции среднее за период равно нулю, т.к. площадь положительной полуволны компенсируется площадью отрицательной. Вводят понятие среднего значения за полупериод при положительной полуволне:
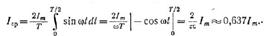
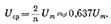
Тепловое действие тока пропорционально квадрату силы тока. О величине его действия судят по среднеквадратичному или действующему (эффективному) значению за весь период. Среднеквадратичное значение периодической функции:
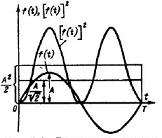
| 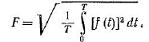 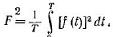 Для периодических токов и напряжений действующие значения:
Для периодических токов и напряжений действующие значения:
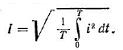 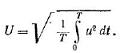
| |
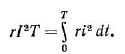
| Действующее значение периодического тока равно такому постоянному току, который, проходя через сопротивление r, за период времени Т выделяет такое же количество теплоты, что и данный ток i/ |
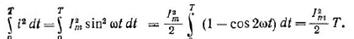
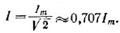
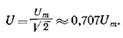
 2017-10-25
2017-10-25 373
373








