Рассмотрим обыкновенное дифференциальное уравнение первого порядка вида (2):
 = f (x, y).
= f (x, y).
Учитывая, что  =
=  , запишем это уравнение в виде
, запишем это уравнение в виде
 = f (x, y).
= f (x, y).
Умножим его на величину  , получим
, получим 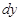 = f (x, y)
= f (x, y)  , откуда имеем
, откуда имеем
f (x, y)  -
- 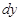 = 0.
= 0.
Получившееся уравнение можно рассматривать как уравнение вида
М (x, y)  + N (x, y)
+ N (x, y) 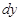 = 0. (7)
= 0. (7)
Пусть каждая из функций М (x,y) и N (x,y) является произведением двух функций, из которых одна зависит только от x, а вторая — только от y:
М (x, y) = М 1(x) М 2(y), N (x, y) = N 1(x) N 2(y),
тогда уравнение (7) принимает вид
М 1(x) М 2(y)  + N 1(x) N 2(y)
+ N 1(x) N 2(y) 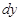 = 0 (8)
= 0 (8)
и называется уравнением с разделяющимися переменными.
Разделим (8) на величину М 2(y) N 1(x), получим
 (9)
(9)
или, введя обозначения  ,
,
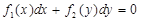 . (10)
. (10)
Уравнения вида (9) или (10) называются уравнениями с разделенными переменными. В них множитель перед  — функция только одной переменной x, а множитель перед
— функция только одной переменной x, а множитель перед 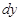 — функция только одной переменной y.
— функция только одной переменной y.
Итак, уравнение с разделяющимися переменными (8) сводится к уравнению с разделенными переменными (9) путем деления обеих частей уравнения (8) на произведение М 2(y) N 1(x). Эта операция называется разделением переменных.
Интегрируем (10), получим решение (интеграл) уравнения (2):
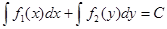 .
.
Таким образом, решение дифференциального уравнения с разделяющимися переменными состоит в выполнении двух действий:
1) разделить переменные, т.е. получить уравнение вида (9) или (10);
2) проинтегрировать уравнение с разделенными переменными.
Пример. Решить дифференциальное уравнение  .
.
Решение. Данное уравнение является обыкновенным дифференциальным уравнением первого порядка с разделяющимися переменными. Разделим переменные x и y:
 ,
,  .
.
Интегрируем:  , откуда получим
, откуда получим
 .
.
Таким образом,  — общее решение.
— общее решение.
Пример 2. Найти частное решение дифференциального уравнения (1 + y 2) dx – xy dy = 0, удовлетворяющее начальному условию у (1) = 0.
Решение. Данное уравнение является обыкновенным дифференциальным уравнением первого порядка с разделяющимися переменными.
1. Найдем сначала общее решение. Для этого разделим переменные x и y:
(1 + y 2) dx = xy dy,
 .
.
Проинтегрируем последнее равенство:  , получим
, получим  . Учитывая свойства логарифмов, общее решение данного уравнения можно записать в виде
. Учитывая свойства логарифмов, общее решение данного уравнения можно записать в виде
 , где
, где 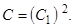
2. Найдем частное решение. Для этого подставим в общее решение начальные условия
x = 1, y = 0, получим С = 1.
Подставим в общее решение найденные значения постоянной С, получим частное решение данного уравнения: x 2 – y 2 = 1.
Пример решения прикладной задачи с помощью дифференциального уравнения с разделяющимися переменными.
Задача. Охлаждение тела.
Пусть в начальный момент тело массой m имеет температуру Т 0. Температура окружающей среды постоянна и равна  Т с, Т 0 > Т с. Найти закон охлаждения тела.
Т с, Т 0 > Т с. Найти закон охлаждения тела.
Решение. При решении используется закон Ньютона (для охлаждающего тела): скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды.
Если  — температура тела в любой момент времени t,
— температура тела в любой момент времени t,  — скорость изменения температуры тела, то
— скорость изменения температуры тела, то  — закон Ньютона. Для охлаждающегося тела:
— закон Ньютона. Для охлаждающегося тела:

где  — коэффициент пропорциональности,
— коэффициент пропорциональности,  .
.
Интегрируем уравнение, разделив переменные:  ,
, 
 ,
, 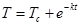
 , где
, где 
Введем начальное условие. При 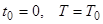

Решение задачи Коши:
 .
.
 2017-10-25
2017-10-25 1396
1396
