Рассмотрим дифференциальное уравнение вида
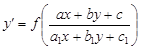 (16)
(16)
где a, b, c, a 1, b 1, c 1 — постоянные, f — непрерывная функция.
Если c = c 1=0, то уравнение (16) является однородным и интегрируется как указано в п. 1.3. Если хотя бы одно из чисел c или c 1 отлично от нуля, то рассмотрим два случая.
1. Определитель 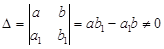 .
.
Введем новые переменные u и v по формулам:
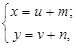
где числа m и n найдем из системы:
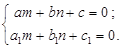
Так как  =
= 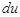 ,
, 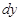 =
= 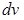 , то уравнение (16) можно привести к однородному уравнению вида (15) относительно функции v (u):
, то уравнение (16) можно привести к однородному уравнению вида (15) относительно функции v (u):
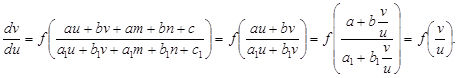
Полученное уравнение интегрируется как указано в п. 1.3.
2. Определитель  . Тогда
. Тогда 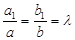 ,
,
и, следовательно, a 1 x + b 1 y = 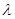 (ax +by). Уравнение (16) примет вид:
(ax +by). Уравнение (16) примет вид:
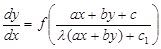 .
.
Подстановкой u (x) = ax + by (x) это уравнение можно привести к уравнению с разделяющимися переменными и решить его как указано в п. 1.2.
Пример. Решить дифференциальное уравнение:
(x + y + 1)  + (2x +2 y - 1) dy = 0.
+ (2x +2 y - 1) dy = 0.
Решение. Данное уравнение можно привести к виду (16):
(2 x + 2y - 1) dy = - (x + y + 1) dx, 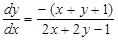 .
.
Так как Δ = 0 и 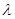 = – 2 (случай 2), то данное уравнение можно привести к уравнению с разделяющимися переменными. Решим его с помощью подстановки.
= – 2 (случай 2), то данное уравнение можно привести к уравнению с разделяющимися переменными. Решим его с помощью подстановки.
Пусть u (x) = - x - y (x), тогда du = - dx - dy, уравнение примет вид
(1 - u) dx + (-2 u - 1)(- dx - du) = 0.
Преобразуем его:
(1 - u) dx + (2 u + 1) dx + (2 u + 1) du = 0,
(2 + u) dx = - (2 u + 1) du.
Таким образом, получили уравнение с разделяющимися переменными. Разделим переменные: dx = - (2 u + 1)/ (2 + u) du.
Проинтегрируем: 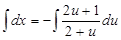 , откуда получим
, откуда получим
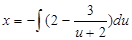 ;
; 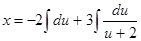 .
.
После преобразований получим общее решение данного уравнения:
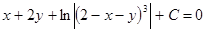 .
.
 2017-10-25
2017-10-25 1911
1911







