2017-11-30
238
Абсолютные показатели вариации
К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
Размах вариации – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака. Зависимость для его расчета имеет вид
,
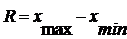где xmax; xmin - наибольшее (наименьшее) значение признака в совокупности
Основным недостатком показателя является то, что он не отражает отклонений всех значений признака.
Среднее линейное отклонение - показатель, отражающий на сколько в среднем каждое значение признака отклоняется от средней величины и представляет собой обобщенную характеристику степени колеблемости признаков совокупности.
A) простое среднее линейное отклонение для не сгруппированных данных
, ()
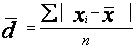где n – число наблюдений признака.
б) взвешенное среднее линейное отклонение для интервального вариационного ряда
. ()
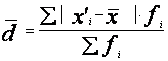При расчете показателя среднего линейного отклонения приходится иметь дело с модулями алгебраических выражений, что при упрощенных конечных выражениях может приводить к ошибкам и неточностям.
Более удобно использовать показатели вариации, найденные с использованием вторых степеней отклонений.
Полученная при этом мера вариации называется дисперсией (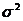
), а корень квадратный из дисперсии – средним квадратическим отклонением (
).
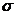Дисперсия - средняя величина квадратов отклонений индивидуальных значений признака от их средней величины.
Рабочие зависимости для расчета дисперсии имеют вид:
