В частных случаях движения
· Поступательное движение АТТ.
В случае поступательного движения АТТ все ее точки движутся с одинаковыми скоростями, равными скорости движения центра масс АТТ: 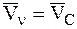 . В случае поступательного движения НМС примет вид:
. В случае поступательного движения НМС примет вид:
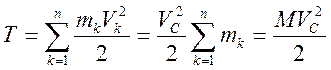 . (7.7)
. (7.7)
· Вращательноедвижение АТТ вокруг неподвижной оси z.
В случае вращательногодвижения АТТ все ее МТ движутся со скоростями 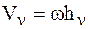 , где
, где 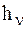 - кратчайшее расстояние от n-й МТ до оси вращения. В случае вращательногодвижения АТТ вокруг неподвижной оси z примет вид:
- кратчайшее расстояние от n-й МТ до оси вращения. В случае вращательногодвижения АТТ вокруг неподвижной оси z примет вид:
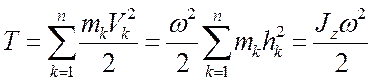 . (7.8)
. (7.8)
· Плоскопараллельноедвижение АТТ.
В случае плоскопараллельногодвижения АТТ в каждый момент времени движение АТТ можно рассматривать как мгновенное вращательное движение относительно оси, перпендикулярной неподвижной (основной) плоскости и проходящей через мгновенный центр скоростей 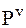 .
.
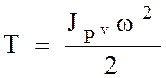 ,
,
где 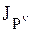 – момент инерции АТТ относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через мгновенный центр скоростей.
– момент инерции АТТ относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через мгновенный центр скоростей.
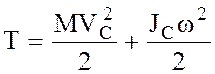 , (7.9)
, (7.9)
где 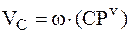 – скорость центра масс АТТ.
– скорость центра масс АТТ.
Теорема Кенига
Теорема: Кинетическая энергия СМТ в общем случае движения равна сумме кинетической энергии центра масс в предположении, что в нем сосредоточена вся масса СМТ, и кинетической энергии СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.
Доказательство.
Введем подвижную систему отсчета с началом в центре масс С, движущуюся поступательно относительно основной инерциальной системы отсчета. Представим скорость n-й МТ, входящей в СМТ, относительно основной системы отсчета в виде (Ч.1 Кинематика):
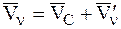 ,
,
где 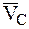 – скорость движения центра масс СМТ, а
– скорость движения центра масс СМТ, а 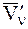 – скорость n-й точки СМТ по отношению к подвижной системе отсчета.
– скорость n-й точки СМТ по отношению к подвижной системе отсчета.
Подставив это выражение в соотношение получим:
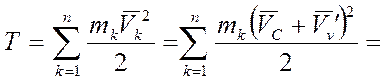
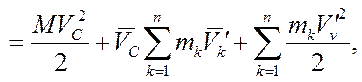
где 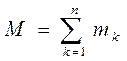 – масса всей системы,
– масса всей системы, 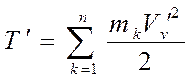 – кинетическая энергия СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.
– кинетическая энергия СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.
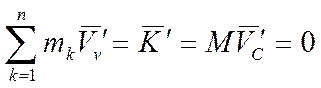 , так как
, так как 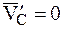 .
.
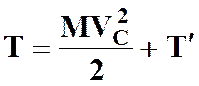 . (7.10)
. (7.10)
 2017-10-25
2017-10-25 1496
1496








