В процессе экспериментальных исследований получается статистический ряд измерений двух величин, когда каждому значению функции y1, у2, …, уn соответствует определенное значение аргумента х1, х2, …, хn..
На основе экспериментальных данных можно подобрать алгебраические выражения функции
y = f(x), (7)
которые называют эмпирическими формулами. Такие формулы подбираются лишь в пределах измеренных значений аргумента x1 – хn и имеют тем большую ценность, чем больше соответствуют результатам эксперимента.
Необходимость в подборе эмпирических формул возникает во многих случаях. Так, если аналитическое выражение (7) сложное, требует громоздких вычислений, составления программ для ЭВМ или вообще не имеет аналитического выражения, то эффективнее пользоваться упрощенной приближенной эмпирической формулой.
Эмпирические формулы должны быть по возможности наиболее простыми и точно соответствовать экспериментальным данным в пределах изменения аргумента. Таким образом, эмпирические формулы являются приближенными выражениями аналитических формул. Замену точных аналитических выражений приближенными, более простыми называют аппроксимацией, а функции – аппроксимирующими.
Процесс подбора эмпирических формул состоит из двух этапов.
I этап. Данные измерений наносят на сетку прямоугольных координат, соединяют экспериментальные точки плавной кривой и выбирают ориентировочно вид формулы.
II этап. Вычисляют параметры формул, которые наилучшим образом соответствовали бы принятой формуле. Подбор эмпирических формул необходимо начинать с самых простых выражений. Так, например, результаты измерений многих явлений и процессов аппроксимируются простейшими эмпирическими уравнениями типа
у = а + bх, (8)
где a, b – постоянные коэффициенты. Поэтому при анализе графического материала необходимо по возможности стремиться к использованию линейной функции. Для этого применяют метод выравнивания, заключающийся в том, что кривую, построенную по экспериментальным точкам, представляют линейной функцией.
Для преобразования некоторой кривой (7) в прямую линию вводят новые переменные
X = f1 (x,y), Y = f2(x,y). (9)
В искомом уравнении они должны быть связаны линейной зависимостью
Y = а + bX. (10)
Значения X и Y можно вычислить на основе решения системы уравнений (9). Далее строят прямую (рис. 8), по которой легко графически вычислить параметры а (ордината точки пересечения прямой с осью Y) и b (тангенс угла наклона прямой с осью X): b = tga = (Yi – a)/Xi.
При графическом определении параметров а и b необходимо, чтобы прямая (8) строилась на координатной сетке, у которой началом является точка Y = 0 и
X = 0. Для расчета необходимо точки Yi и Xi принимать на крайних участках прямой.
 |
Рис. 8. Графическое определение параметров X и Y
Для определения параметров прямой можно применить также другой графический метод. В уравнение (10) подставляют координаты двух крайних точек, взятых с графика. Получают систему двух уравнений, из которых вычисляют а и b. После установления параметров а и b получают эмпирическую формулу (8), которая связывает Y и X, позволяет установить функциональную связь между х и у и эмпирическую зависимость (7).
Линеаризацию кривых можно легко осуществить на полулогарифмических или логарифмических координатных сетках, которые сравнительно широко применяют при графическом методе подбора эмпирических формул.
Пример. Подобрать эмпирическую формулу следующих измерений:
1 2 3 4 5 6 7
12,1 19,2 25,9 33,3 40,5 46,4 54,0
Графический анализ этих измерений показывает, что в прямоугольных координатах точки хорошо ложатся на прямую линию и их можно выразить зависимостью (8). Выбираем координаты крайних точек и подставляем в (8). Тогда A0 + 7 A1 = 54,0; A0 + 1 A1 = 12,1, откуда А1 = 41,9: 6 = 6,98 и А0 = 12,1 – 6,98 = 5,12. Эмпирическая формула примет вид
y = 5,12 + 6,98 х.
Таким образом, аппроксимация экспериментальных данных прямолинейными функциями позволяет просто и быстро установить вид эмпирических формул.
Графический метод выравнивания может быть применен в тех случаях, когда экспериментальная кривая на сетке прямоугольных координат имеет вид плавной кривой. Так, если экспериментальный график имеет вид, показанный на рис. 9а, то необходимо применить формулу
у = а ·х  (11)
(11)

Рис. 9. Основные виды графиков эмпирических формул
Заменяя X = lg х и Y = lg у, получим Y = lg a – bХ. При этом экспериментальная кривая превращается в прямую линию на логарифмической сетке. Если экспериментальный график имеет вид, показанный на рис. 9б, то целесообразно использовать выражение
у = а ·е  . (12)
. (12)
При замене Y = lg у получим Y = lg a + bx lg e. Здесь экспериментальная кривая превращается в прямую линию на полулогарифмической сетке. Если экспериментальный график имеет вид, представленный на рис. 9в, то эмпирическая формула принимает вид
у = с + ахb. (13)
Если b задано, то надо принять X = хb, и тогда получим прямую линию на сетке прямоугольных координат Y = с + а X. Если же b неизвестно, то надо принять X = lg х и Y = lg (y – с), в этом случае будет прямая линия, но на логарифмической сетке Y = lg a + bХ. В последнем случае необходимо предварительно вычислить с. Для этого по экспериментальной кривой принимают три произвольные точки (х1, у1), (х2, у2), и (х3 =  , y3) ивычисляют с в виде отношения
, y3) ивычисляют с в виде отношения
с = (у1 у2 – y32): (у1 + у2 –2уз) (14)
Если экспериментальный график имеет вид, показанный на рис. 9.4г, то нужно пользоваться формулой
y = с + а ebx. (15)
Путем замены Y = lg (у – с) можно построить прямую на полулогарифмической сетке
Y = lg a + bx lg c,
где с предварительно определено с помощью формулы (14). В этом случае
х3 = 0,5(х1 + х2).
Если экспериментальный график имеет вид, представленный на рис. 9.4д, то применяется выражение
у = а + b/х. (16)
Путем замены х = 1 / z можно получить прямую линию на сетке прямоугольных координат у = а + bz.
Если график имеет вид, соответствующий кривым на рис. 9е, то используют формулу
y = 1/(a + bx). (17)
Если принять новую функцию у = 1/z, где z = а + bх, то получится прямая на сетке прямоугольных координат «z – х».
Аналогично, уравнению
y = 1/(а + bх + сх2) (18)
путем замены y = 1/z можно придать вид параболы z = а + bх + сх2.
Сложную степенную функцию
y = а e  (19)
(19)
можно преобразовать в более простую. При lg у = z; lg a = р; п lg e = q;
т lg е = r получается зависимость
z = р + qx + r х2.
С помощью приведенных на рис. 9 графиков и выражений (11 – 19) можно практически всегда подобрать уравнение эмпирической формулы.
Пример. Необходимо подобрать эмпирическую формулу для следующих измерений:
1 1,5 2,0 2,5 3,0 3,5 4,0 4,5
15,2 20,6 27,4 36,7 49,2 66,0 87,4 117,5
На основе этих данных строится график (рис. 9а), соответствующий кривым (12) (рис. 9б).
После логарифмирования выражения (12) lg у = lg a + bx lg e. Если обозначить lg у = Y, то Y = lg a + bx lg e, т. е. в полулогарифмических координатах выражение для Y представляет собой прямую линию (рис. 10). Подстановка в уравнение координат крайних точек дает
lg 15,2 = lg a +b lg е и lg 117,5 = lg a + 4,5 b lg e.
Следовательно, lg a + b lg е = 1,183; lg a + 4,5 b lg e = 2,070.
Откуда b = 0,887/(3,5 lg e) = 0,583; lg a =1,183 – 0,254 = 0,929; a = 8,492. Окончательно эмпирическая формула получит вид
У = 8,492 е  .
.
При подборе эмпирических формул широко используются полиномы
у = Ао + А1 х + А2 х2 + А3 х3 +...+Аn хn (20)
где Ао, A1,..., Аn – постоянные коэффициенты. Полиномами можно аппроксимировать любые результаты измерений, если они графически выражаются непрерывными функциями. Особо ценным является то, что даже при неизвестном точном выражении функции (20) можно определить значения коэффициентов А. Для определения коэффициентов А кроме графического метода, изложенного выше, применяют также методы средних и наименьших квадратов.
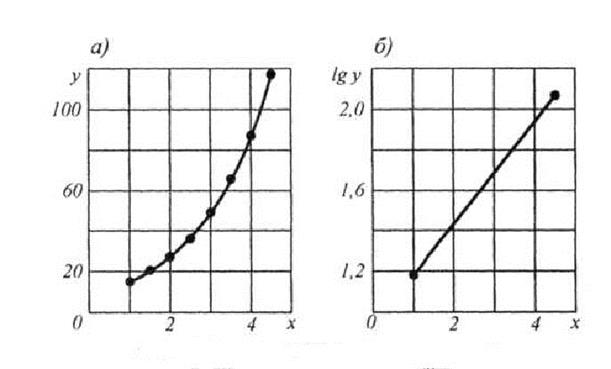
Рис. 10. Подбор эмпирической характеристики:
а – эмпирическая; б – спрямленная
9.4. Элементы теории планирования эксперимента
Математическая теория эксперимента определяет условия оптимального проведения исследования, в том числе и при неполном знании физической сущности явления. Для этого используются математические методы при подготовке и проведении опытов, что позволяет исследовать и оптимизировать сложные системы и процессы, обеспечивать высокую эффективность эксперимента и точность определения исследуемых факторов. Обеспечивается также эффективное управление экспериментом при неполном знании механизма явлений.
Эксперименты обычно ставятся небольшими сериями по заранее согласованному алгоритму.
После каждой небольшой серии опытов производится обработка результатов наблюдений и принимается строго обоснованное решение о том, что делать дальше.
При использовании методов математического планирования эксперимента возможно решать различные вопросы, связанные с изучением сложных процессов и явлений; проводить эксперимент с целью адаптации технологического процесса к изменяющимся оптимальным условиям его протекания и обеспечивать, таким образом, высокую эффективность его осуществления и др.
Теория математического эксперимента содержит ряд концепций, которые обеспечивают успешную реализацию задач исследования. К ним относятся концепции рандомизации, математического моделирования, последовательного эксперимента, оптимального использования факторного пространства и ряд других.
Принцип рандомизации заключается в том, что в план эксперимента вводят элемент случайности. Для этого план эксперимента составляется таким образом, чтобы те систематические факторы, которые трудно поддаются контролю, учитывались статистически и затем исключались в исследованиях как систематические ошибки.
При последовательном проведении эксперимент выполняется не одновременно, а поэтапно, с тем, чтобы результаты каждого этапа анализировать и принимать решение о целесообразности проведения дальнейших исследований (рис. 11).
В результате эксперимента получают уравнение регрессии, которое часто называют моделью процесса. Для конкретных случаев математическая модель создается исходя из целевой направленности процесса и задач исследования, с учетом требуемой точности решения и достоверности исходных данных, что обычно производится по критерию Фишера. Так как степень полинома, адекватно описывающего процесс, предсказать невозможно, то сначала пытаются описать явление линейной моделью, а затем, если она неадекватна, повышают степень полинома, т. е. проводят эксперимент поэтапно.
В настоящее время изданы каталоги планов эксперимента, например каталог планов, выпущенный Московским государственным университетом, в которых приводится сравнительная оценка планов и рекомендации по их выбору применительно к конкретным условиям эксперимента.
Важное место в теории планирования эксперимента занимают вопросы оптимизации исследуемых процессов, свойств многокомпонентных систем или других объектов. Как правило, нельзя найти такое сочетание значений влияющих факторов, при котором одновременно достигается экстремум всех функций отклика. Например, максимальный крутящий момент двигателя и минимальный расход топлива достигаются при различных режимах работы. Поэтому в большинстве случаев за критерий оптимальности выбирают лишь одну из переменных состояния − функцию отклика, характеризующую процесс, а остальные принимают приемлемыми для данного случая. Методы планирования эксперимента в настоящее время быстро развиваются, чему способствует возможность широкого использования ЭВМ.
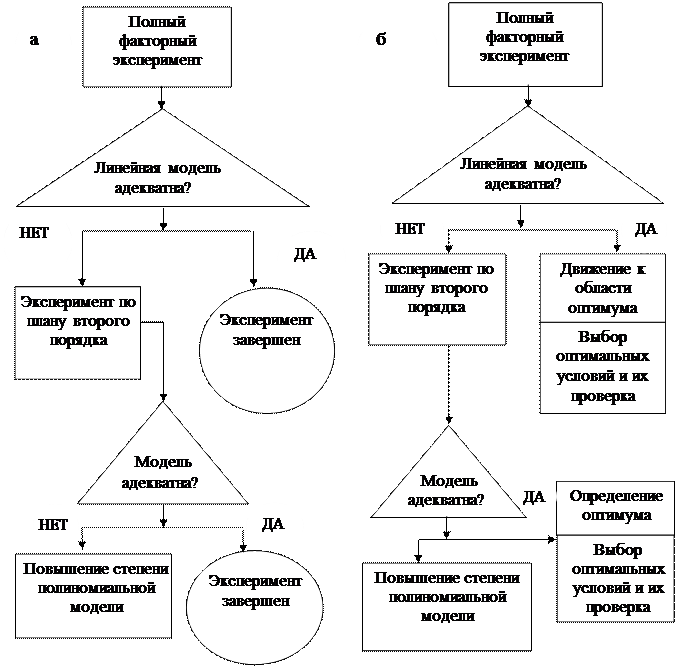
Рис. 11. Структурная схема эксперимента:
а – с целью математического описания исследуемого процесса; б – с целью оптимизации исследуемого процесса
 2017-10-25
2017-10-25 6967
6967








